Ch8. Visualizing Model Performance
- 숙명여자대학교 소프트웨어학부 데이터사이언스개론 - 박동철 교수님
# Visualizing Model Performance
- 모든 사람들이 model performance를 이해하는 데 있어 동일한 background를 가지고 있는 것은 아니므로 시각화 필요
- model performance에 대해 더 직관적인 이해를 가능하게 해 줌

> 위의 그래프는 많이 휘어질수록 좋은 성능을 보임
# Ranking Instead of Classifying
- 이전에서 배운 modeling은 어떻게 classfy 할 것인가? 에 초점
- chapter 8에서는 성능을 시각화하는 방법에 대해 배울 것
- classifier가 직접 return 하는 하나의 specific 한 값에 의미를 두지 않고 ranking의 개념으로 성능을 바라볼 것임
- ranking: 같은 데이터를 다른 각도에서 바라봄 = sorting
> predicted scores and take the top n cases
- 일반적으로 ranking을 하는 이유
> 우리는 가장 보장이 되는 case n개를 원함
ex) 한정된 예산으로 마케팅을 할 때 가장 response 할 것 같은 상위 n명에게만 마케팅을 함
> 각각의 확률 값을 정확하게 계산하는 것보다 상대적으로 정렬을 한 후 선택한 상위 n개가 중요해짐
# Ranking Instances
- instance에 대해 score를 주는 classifier가 있음
- score를 기준으로 instance를 정렬하고 특정 값에 따라 임계값 설정
→ ex) 상위 20%에게만 마케팅 제공, 상위 n명 아래로는 서비스 X 등..

> score: 어떤 기준을 가지고 값을 매김
> 임계값 T를 높게 잡으면 특정한 case에 대해서만 얻을 수 있음
> 임계값 T를 낮게 잡으면 가능한 많은 case를 얻을 수 있음
# Thresholding Instances
- threshold가 바뀔 때마다, true positive와 false positive의 수가 바뀜
> 각 threshold가 specific confusion matrix를 결과로 만들어 냄
- ex) instance가 200개인 예시
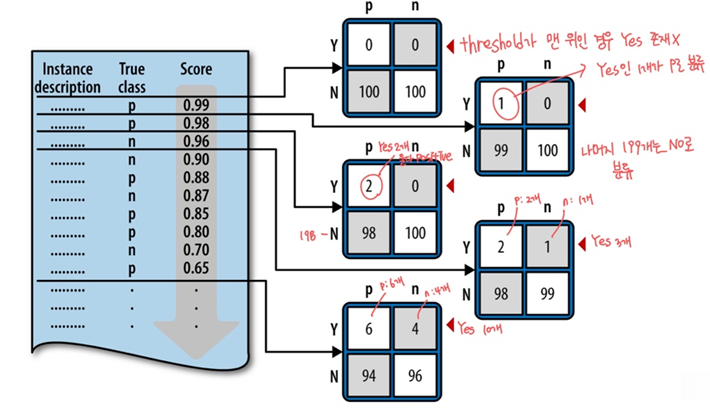
- oservations
> 임계선이 낮아질수록 (N, p) → (Y, p), (N, n) → (Y, n)로 이동
> 다른 임계선은 다른 classifier를 가짐 →
임계선이 confusion matrix를 나타내는데 confusion matrix가 다르면 classifier도 다르기 때문임
- 두 가지 질문
> 다른 방법으로 sorting 해서 매긴 ranking 간의 비교는 어떻게 해야 하는가?
> 적절한 임계선(threshold)은 어떻게 고를 수 있는가? → 기대 이익을 극대화하는 임계선 선택
# Profit Curve
- 각 threshold로부터 만들어지는 expected profit을 보여주는 것
> threshold를 낮게 잡을수록 positive라고 예측하는 비율은 증가

> x축: threshold를 어떻게 잡는가?
> y축: profit
# EX) Profit Curve
- each Profit Curve: 제안을 수용할 가능성이 높은 사람부터 낮은 사람까지 순서를 매긴 것
- 관심 있는 부분에 대해서만 이야기 가능

- curves는 profit이 음수가 될 수 있음을 보여줌 (항상 그런 것은 X)
> margin(남는 이익)이 작고 marketing에 반응하는 사람이 적을 때 발생

> 물건 값: $9, marketing 하는 데 사용하는 우표: $5
> True positive: margin = 4 (9-5)
> False positive: -5 (우표값)
- 모든 사람들에게 offer를 제공했기 때문에 100% 일 때 profit이 같음

→ 실제 P/N의 확률은 고정되어있기 때문임
- classifier의 차이에 따라 sorting의 결과가 다르기 때문에 customer들의 순서가 달라지며 그에 따른 profit에도 차이가 생김
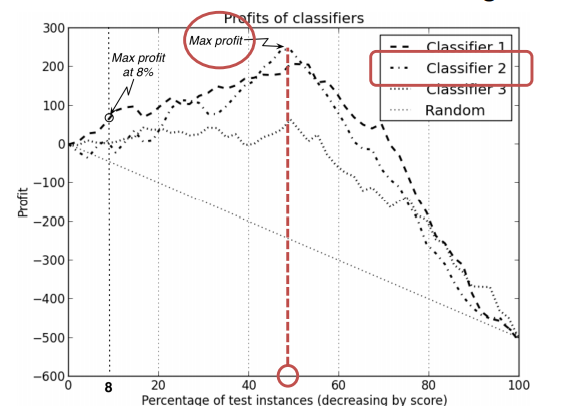
> Random: 응답자를 random 하게 잡기 때문에 성능이 좋지 못함
> Classifier2: 예산의 제한이 없을 때 Max profit을 만들어내는 threshold의 위치는 50%이며
그때 사용되는 classifier는 classifier2 임
- 예산에 제한이 있을 때

> 고객이 100000명 예산이 $40000이며 한 명에게 marketing 하는 비용이 $5라면
우리는 상위 8%(8000)에게 marketing이 가능함
> threshold가 8% 일 때 Max profit을 보이는 classifier는 classifier1 임
# Limitation of Profit Curves
- profit curves에는 두 가지 조건이 존재

> 사전 class는 미리 알아야 하며 안정적이어야 함
→ 변경되면 expected profit도 계속 변경되기 때문
> cost와 benefit도 미리 알아야하며 안정적이여야 함
- 하지만 많은 분야에서 사전 class와 cost&benefit이 특정한 값으로 정해 지거나 안정적이지 않음
> 사기 탐지 → 사기마다 발생 시간, 금액 등등 바뀌는 것이 많음
> 고객 이탈 관리 → 제안마다 다른 cost 발생
# Receiver Operating Characteristic (ROC) Graph
- profit curve에서 수용하지 못하던 uncertainty를 수용할 수 있음
- benefit(true positives)와 cost(false positive) 사이의 상대적인 trade-off를 보여줌

> ROC graph는 5개의 classifier(A, B, C, D, E)의 성능을 보여줌
> profit curve에서 하나씩 새로 그려야 했던 그래프를 여기서는 점 하나로 표현 가능
# Representing A Classifier in ROC Space
- ROC space에서 각 classifier는 하나의 점으로 표현 (fpr, tpr)
> x축: Flase positive rate (=1-specificity) 즉, negative 중 틀린 것
> y축: True positive rate = sensitivity 즉, positive인 것 중에 맞은 것

- ROC가 임상병리 쪽에서 많이 쓰이기 때문에 그들이 편한 용어인 민감도, 특이도와 같은 용어를 사용하는 것임
# Notable Points in ROC space
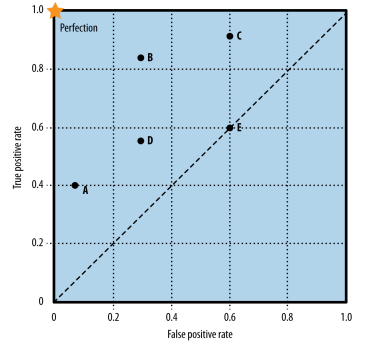
> (0, 0): classifier가 무조건 negative라고 예상 (No)
> (1, 1): classifier가 무조건 positive라고 예상 (Yes)
> (0, 1): Positive는 Yes, negative는 no라고 완벽하게 예측하는 classifier
# The Diagonal in ROC space
- (x, x): positive class를 x·100%로 랜덤 하게 추측

> True positve도 60%로 맞추지만, False positive도 60%로 틀리게 예측하는 것
# Comparing Classifiers in ROC space
- superior: 비교 대상보다 false positive rate는 낮고, true positive rate은 높은 것
- conservative: lower - left hand 즉 Yes라고 예측하는 비율이 No라고 예측하는 비율보다 적은 것
- permissive: Yes라고 예측하는 비율이 No라고 예측하는 비율보다 많은 것

> B는 E보다 superior 함
> A는 B보다 conservative 하고 B는 C보다 conservative 함
> C는 B보다 permissive 하고 B는 A보다 permissive 함
# ROC Curve for A Ranking Model
- Ranking model
> classifier의 score가 threshold 위에 있으면 Y(es)로, 아래 있으면 N(o)로 분류됨
> threshold에 따라 confusion matrix가 달라지기 때문에 ROC 영역에 다른 point를 만듦
> threshold가 낮아지면 낮아질수록 positive instance와 negative instance가
동시에 증가하기 때문에 true positive의 비율과 false positive의 비율이 함께 증가함

> 우상향 하는 이유: true positive와 false positive rate이 동시에 증가하기 때문
# (EX) Construction of a ROC Curve
- ROC Curve: 전체 classifier의 성능이 어느 점에 해당하는지 한눈에 보여줌
- threshold가 낮아질수록 confusion matrix가 달라짐 → ROC Curve에서의 performance가 달라짐

> 그래프가 앞에서와는 반대로 그려져 있음 threshold가 위로 올라가는 것이
사실은 threshold를 낮추는 것
# Advantage of ROC Curves
- classifier의 성능과 사전 class 그리고 benefit & cost와는 구별됨
- 사전 class 그리고 benefit & cost가 변해도 상대적인 성능 (curve)에 있어 차이는 없을 것임
→ point 자체의 위치는 달라질 수 있지만 성능은 변하지 않는다는 장점

# The Area Under the ROC Curve (AUC)
- ROC curve 아래쪽의 면적 → 0부터 1 사이의 값을 가짐
- AUC는 performance를 요약하는 single number(performance number)가 필요할 때 유용함
ex) A가 B보다 0.1 정도 성능이 더 높다
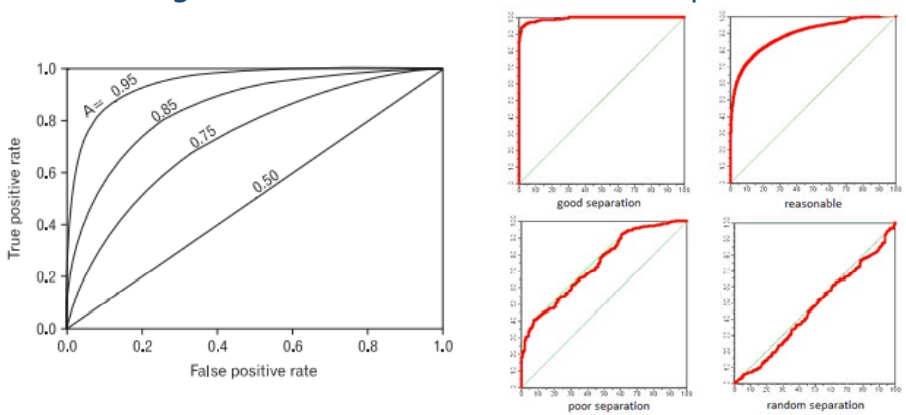
> (0, 1)에 curve가 가까울수록 성능이 좋은 것임
> curve가 대각선 아래로 내려가면 실질적으로 사용할 필요가 없다고 생각하면 됨
# Cumulative Response Curve
- ROC curves
> 이해관계자들 중 전문가가 아닌 사람에게 설명할 때 사용하기에는 한계가 있음
- Cumulative Response Curves
> 더 직관적임
> positive인 것을 yes라고 얼마만큼 잘 분류했는지가 중요

> 원래 ROC의 x축: false positive rate
> Cumulative Response Curves: threshold의 상대적인 위치
- 직관
> 모든 instance에 대해서 x%로 target을 하면, (true) positive에 대해 x%를 얻음
> 대각선보다 위에 있는 curve = x%로 target 했을 때, positive에 대해 x%보다 더 높게 얻음
* 대각선 = random
> 대각선보다 위에 있는 curve는 이점이 더 많음
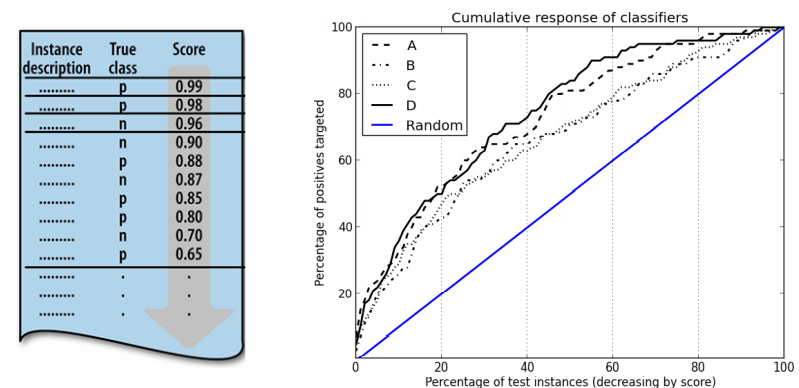
# The Lift of A Classifier
- cumulative response curve의 단점을 보완
- Lift: classifier의 advantage
- positive를 올리고 negative를 아래로 내림
- 얼마만큼 아래 그림에서의 오른쪽과 같이 분류할 수 있는지? ← Lift
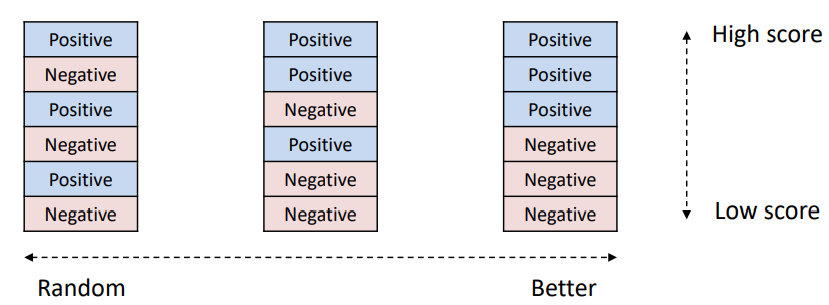
- 정의

ex) 50% targeting 했을 때 그중에서 몇 %가 positive인가?
# (EX) The Lift of A Classifier
- 100명의 고객이 있고 이 중 50명이 positive, 50명이 negative라고 가정
- 50%의 고객만 targeting을 할 때, positive는 몇 %를 차지하는지?
- case1: random으로 분류
> 랜덤이므로 해당 50% 안에 랜덤 하게 섞여 있으므로 positive가 절반일 것
> lift = 0.5 / 0.5
- case 2: 그래도 random보다는 성능이 좋음
> lift > 1 // 분자가 random보다는 클 테니까!
- case 3: classifier가 완벽한 성능을 보임
> 50%를 positive가 100% 차지하고 있음
> lift = 1.0 / 0.5
# Lift Curve
- cumulative response of classifier는 어떤 classifier가 더 성능이 좋은지 한눈에 들어오지 X
- lift = x point에 주어진 cumulative response의 값 / 주어진 x
= x point가 가리키는 percentage of positive / x가 가리키는 random point

> cumulative response of classifier는 우 상향하면서 성능이 커짐
> lift curve에서 random 모델이 1의 값을 갖는 이유는 random 모델의 lift가 1이기 때문
→ 자기 자신을 자기 자신으로 나누는 것임
- Example: 만약 모델이 2배의 lift를 보인다면?
> 모델의 true positve rate이 random classifier의 true positive 보다 2배 높은 것임
- lift는 targeting의 effectiveness를 보여줌
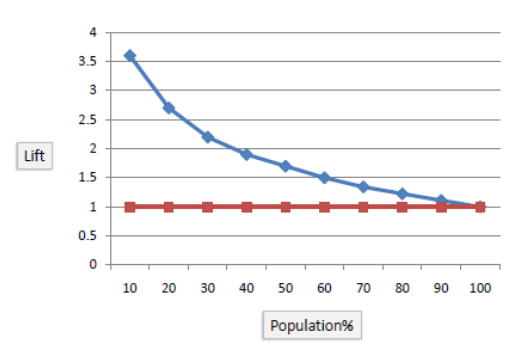
# Exmaple: Performance Analytics
- cell phone churn dataset
> 47,000명의 고객 데이터
> 7%만 churn (positive), 93% not churn (negatives)
- training 하고 모델을 만들어야 할 때 무엇을 사용할 수 있을까?
> classification tree
> logistic regression
> nearest-neighbor model
> navie bayes (나중에 나옴)
- 모델의 성능 측정
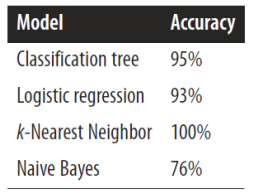
> 같은 dataset에 대하여 test 한 결과이기 때문에 의미 없음
> navie bayes의 정확도는 너무 낮고, k-nn의 정확도는 너무 높음
> 모두 no라고 분류를 했을 때 적어도 93%의 확률이 나와야 하는데 navies bayes는 그렇지 않음
- 10-fold cross validation을 사용해 다시 결과를 측정

> 전체적으로 정확도가 낮아지며 평균과 표준 편차의 값을 알 수 있음
> AUC는 classifier의 성능을 측정하는 도구인데 정확도가 비교적 낮은 navies bayes가 반대로 높게 나옴
- fitting curve

> 모델의 overfitting을 알려줌
> y축이 accuracy대신 AUC
> 노드가 100개일 때 overfitting 발생
- AUC 값을 가지고 분석

> accuracy는 정확하게 성능을 나타내는 지표가 되지 못하므로 AUC를 가지고 분석
- Q1. 모든 AUC의 값은 사용하기에 나쁘지 않은 수치인가?
> 많은 dataset이 예측을 하는데 잘 사용되는 signal이 적음
> 적당한 AUC 값은 사업적인 측면에서 좋은 결과를 이끌 수 있음
- Q2. Navie Bayes가 낮은 accuracy에도 불구하고 높은 AUC를 갖는 이유는?

사진 삭제
사진 설명을 입력하세요.
> AUC에서는 가장 높은 accuracy를 보이는 k-nn의 성능이 가장 낮음
> navie bayes가 yes를 yes라고 예측한 수가 많음
> k-nn은 맞는 것을 예측하지 않음 (모두 no라고 예측) 이는 no가 93%였기 때문에 운 좋게 나온 결과임
즉, baserate이 높아서 정확성이 높았던 것임
> navie bayes는 잘못 예측한 것도 있지만 chuner도 맞춤
- ROC curve
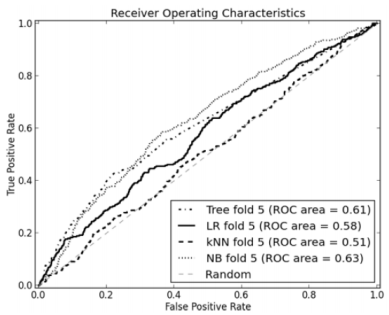
> ROC curve는 (0,1) 쪽에 가까워질수록 좋은 성능
> 어느 만큼 휘었는지 어느 구간에서 어떤 방법이 더 효율적인지 구분이 어려움
> 상대적인 비교를 위해 lift curve를 사용
- Lift Curve

> test instance의 portion이 25% 정도까지는 tree의 성능이 더 좋고 그 이후로는 NB의 성능이 더 좋음
> lift curve는 얼마만큼의 profit을 기대할 수 있는지 알려주지 않음
→ profit curve를 사용하면 cost와 benefit이 주어질 때 기댓값을 알 수 있음
- cost and benefit (9:1의 profit 비율, $27 vs $3)
> v(Y, n) = -3 // 살 거라고 예상해서 marketing 했는데 안삼
> v(N, p) = 0 // 안살 거라고 예상했는데 marketing했으면 살거였던 사람
> v(Y, p) = 27 // 살거라고 예상해서 marketing 해서 삼
> v(N, n) = 0 // 안 살 거라고 예상해서 marketing 안 했는데 안살거였던 사람
- profit curves

> tree가 가장 높은 maximum을 보임
> 25% 이상에서는 NB가 더 높은 성능을 보임
> 전체에서 maximum profit을 원한다면 tree를 선택하면 됨
- cost benefit을 변경 (12:1 $36 vs $3)
> v(Y, n) = -3 // 살거라고 예상해서 marketing을 했는데 안 살 사람이었음
> v(N, p) = 0 // 안살거라고 예상해서 marketing을 안했는데 사실 살 사람이었음
> v(Y, p) = 36 // 살거라고 예상해서 marketing을 했는데 실제로도 살 사람이었음
> v(N, n) = 0 // 안살거라고 예상해서 marketing을 안했는데 안 살 사람이었음
- The new profit curves

> matrix 값 하나 바뀌었을 뿐인데 그래프의 개형이 달라짐
'Study > Data Science' 카테고리의 다른 글
| [DataScience] Ch10. Representing and Mining Text (0) | 2021.08.24 |
|---|---|
| [DataScience] Ch9. Evidence and Probabilites (0) | 2021.08.24 |
| [DataScience] Ch7. Decision Analytic Thinking 1: What is a Good Model? (0) | 2021.08.24 |
| [DataScience] Ch6. Similarity, Neighbors, and Clusters (0) | 2021.08.24 |
| [DataScience] Ch5. Overfitting and Its Avoidance (0) | 2021.08.24 |
