Ch7. Decision Analytic Thinking 1: What is a Good Model?
- 숙명여자대학교 소프트웨어학부 데이터사이언스개론 - 박동철 교수님
# How Would You Measure A Model?
- data를 mining함으로써 무엇을 성취하고자 하는지(=goal)를 고려하는 것은 매우 중요
- 의미있는 방식으로 성능을 측정해야 함
> problem에 대한 "올바른" 평가 metric은 무엇인가?
> (ex) cellular-churn problem → 무엇을 기준으로 성능을 측정할 것인지는 회사나 도메인에 따라 다름.
즉 얻고자하는 정보에 따라 달라질 수 있는 것 → 이탈하는 고객의 비율, 예측 정확도 등등..
# Evaluating Classifiers
- classification model: 새로운 정보가 class에 들어왔을 때 그것의 class를 예측하는 것
- binary classification을 고려해봄: positive, negative
- 우리는 이 모델의 일반적인 성능을 어떻게 측정할 수 있을까?
| Actual: Churn | Actual: Not Churn | |
| predicted: churn | yes라고 예측했는데 실제로도 yes인 것 | yes라고 예측했는데 실제로는 no인 것 |
| predicted: not churn | no라고 예측했는데 실제로는 yes인 것 | no라고 예측했는데 실제로도 no인 것 |
> 우 하향하는 정보들이 중요함
# Plain Accuracy and Its Problems
- classifier의 성능을 측정하기 위해 간단한 metric을 가정 : accuracy (or error rate)
- 정의

> correct: 얼마만큼 제대로 맞췄는가(예측했는가)?
- 측정하고 이해하기에 쉬움
- 너무 단순하고 이미 잘 알려진 문제점을 가지고 있음 (문제점은 뒤에서 언급)
# The Confusion Matrix
- n-class에 대한 confusion matrix는 n*n matrix임
> columns(세로): actual(or true) classes
> rows(가로): predicted classes (예측)
> error의 종류를 각각 보여줌
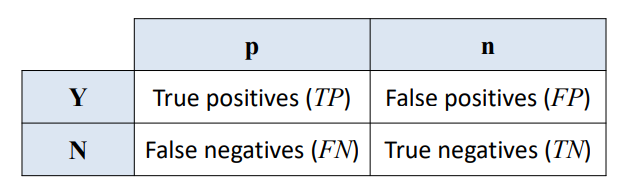
- example: 2*2 confusion matrix

> True positive: 맞다고 예측했는데 실제로도 맞은 것 (예측이 맞음)
> False positive: 맞다고 예측했는데 실제로는 틀린 것 (예측이 틀린 것)
> False negatives: 틀리다고 예측했는데 실제로는 맞은 것 (예측이 틀린 것)
> True negatives: 틀리다고 예측했는데 실제로도 틀린 것 (예측이 맞은 것)
> The error rate = False positives + False negatives
# Problems with Unbalanced Classes
- 한 클래스가 드문 경우의 분류 문제를 고려해보자
> 사기당한 고객을 찾는 것, 불량 부품을 찾는 것, 제안에 응답할 고객을 targeting 하는 것
> 위의 예시는 모두 불균형하거나 치우쳐 있음
- 이런 경우는 accuracy를 기반으로 한 평가에서 잘 동작하지 못함
> 999:1 비율로 클래스가 나타나는 도메인이 있을 경우를 고려해보자
> 가장 만연한 class를 선택하면 99.9%의 정확도를 얻을 수있음
ex) 사기당할 확률이 0.01% 라면 사기당하지 않은 class로만 분류하면 99.9%의 정확도를 얻는 것
> 사소하지 않은 solution을 찾는다면 만족스럽지 못함
- 편중되는 것은 좋지 않으며, accuracy가 잘못된 해석을 이어나갈 수 있음
- Example: cellular-churn problem
> A와 B가 1000명의 고객에 대한 그들만의 churn 예측 모델을 만듦

> A: churn에 대한 정확도는 100%지만, not churn에 대한 정확도는 60% 임
(실제로 churn 한 사람은 모두 churn이라고 올바르게 분류했지만
not churn은 500명 중 300명만 not churn이라고 분류했기 때문)
> B: not churn에 대한 정확도는 100%지만, churn에 대한 정확도는 60% 임
(실제로 not churn 한 사람은 모두 not churn이라고 올바르게 분류했지만
churn은 500명 중 300명만 churn이라고 분류했기 때문)
> 그들의 정확도는 80%로 같지만 각각의 모델이 동작하는 것은 매우 다름. 즉, 성능이 다름
- 서로 다른 dataset을 가지고 위의 두 모델을 비교
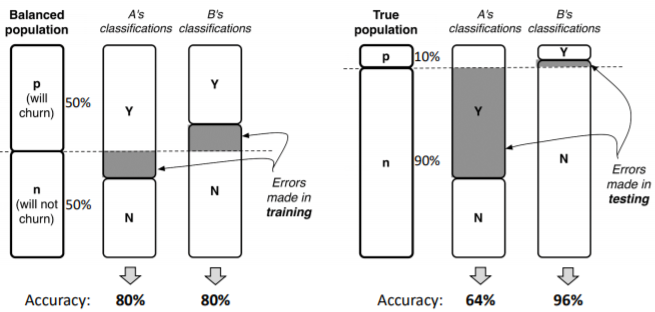
> 새로운 dataset을 가지고 동작한 오른쪽의 예시를 통해 B 모델이 A모델 보다 좋다고 할 수 있는가?
NO! 바꾼 dataset에서 n이 아닌 p의 비율이 더 높았다면 A의 성능이 더 좋은 것으로 측정되기 때문
# Problems with Unequal Costs and Benefits
- 단순한 정확성의 문제점
> false positive와 false negative errors 사이를 구분하지 않음
> 그들을 같이 계산하면 두 가지 오류 모두 똑같이 중요해짐
- 실제 domain에서 위와 같은 경우는 매우 드물음
> errors의 결과가 다르면 그 cost도 다름
- Example (1): 암 진단
> False positive: 암에 걸렸다고 진단했는데 알고 보니 안 걸림
→ 삶에 큰 위협이 되지 않으므로 괜찮음
> False negative: 암에 안 걸렸다고 진단했는데 실제로는 암에 걸렸던 것
→ 심각한 상황
> accuracy, error rate으로만 모델의 성능을 측정하기에는 단점이 존재함
- Example (2): cellur-churn
> False positive: churn 할 것이라고 예상했는데 안 함
→ 스타벅스 기프티콘을 줘서 churn하지 않게 하는 것이 이득이라 기프티콘을 제공하긴 했지만
결론적으로 고객이 churn하지 않았으므로 기업 입장에서는 적은 cost를 지불한 것임
> False negative: churn하지 않을 것이라고 예상했는데 churn 함
→ 기프티콘에 대한 cost보다 고객이 핸드폰을 사지 않았을 때 발생하는 손실이 크므로 손해임
- 대부분의 모든 domain에서, False positive와 False negative의 error를 각각 다르게 다뤄야 함
> classifier가 만드는 결정의 cost 혹은 benefit을 평가해야 함
> 일단 집계되면, classifier에 대한 기대 이익(기대 이득 혹은 기대 비용) 추정을 만들어냄
# Generalizing Beyond Classification
- data science를 적용시킬 때 중요한 질문
> 목표는 무엇인가?
> 목표가 주어진 data mining의 결과를 적절히 평가하고 있는가?
- Example: regression
> 고객이 보지 않은 영화에 대해 별을 얼마나 줄 것인가를 예측하는 모델
> 우리는 이 모델을 어떻게 측정해야 할까? 에러의 평균/에러의 평균의 제곱?
> 우리는 더 나은 metric이 있는지 확인해보아야 함
# (Ex) Metrics for Regression Models

> Mean absolute error: Mean error에서 음수 값이 양수 값을 offset 시키는 문제를 보완함
# A Key Framework : Expected Value (EV)
- 데이터 분석적 사고를 돕는 유용한 개념적 도구로써 우리에게 필요한 지식을 얻는 데 사용함
- 데이터 분석 문제에 대한 생각을 정리하는 데 매우 유용한 핵심 framework를 제공
- 기댓값의 계산
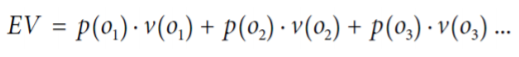
> oi : 내가 원하는 결과
> p(oi) : oi의 확률
> v(oi) : oi의 값
# Using EV for Classifier Use
- Example: target marketing
> 어떤 사람에게 offer를 주었을 때 제안을 받아들일까 안 받아들일까?
> target marketing을 보고 제안을 받아들여야겠다고 생각하는 사람은 매우 적음
> 상식선을 50%라고 결정.
고객이 offer를 받아들이는 확률이 50% 는 되어야 target marketing을 하는 의미가 있음
- 확률의 관점으로만 접근하면 X.
> 기댓값이라는 개념을 써서 만들어보면 위의 생각 (50%는 넘어야 의미가 있다)이
무조건 맞지 않다는 것을 알게 됨
- feature vector가 x인 고객에 대해 pR(x)를 주는 model이 있다고 가정
> pR(x): 고객 x에 대한 응답 확률을 추정한 것
> ex) classification tree, logistic regression model, or some other model
- 그러면 우리는 targeting 하는 고객 x의 기대 이득 혹은 비용을 계산할 수 있음
> expected benefit: 고객이 response를 주었을 때 얼마만큼 돈을 벌 수 있는가?
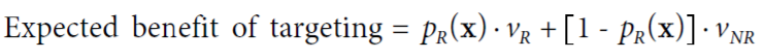
> vR: 응답으로부터 얻는 값. 즉, response로 인해 얻는 이득
> vNR: 응답이 없을 때 얻는 값. 즉, no response일 때 드는 비용
- Example scenario
> 물건 값 200$
> 원가 100$
> target marketing에 드는 비용 1$ (우표값임)
- Example scenario 기댓값 계산
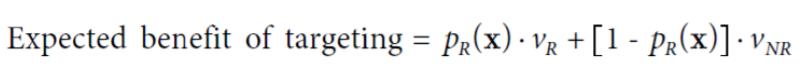
> vR: $99 (target marketing에 성공했을 때 얻는 이득)/ 원가 - 우표값
> vNR: -$1 (target marketing에 실패했을 때의 비용) / 우표값이 cost로 발생
- 기댓값이 0보다만 크면 남는 장사임

> customer 중 1%만 응답해도 우리는 이득이다. 즉, 100중 1명만 응답해도 이득
* 50% 이상이 중요한 게 아님
# Using EV for Classifier Evaluation
- 그 모델이 decision making을 하는 set 전체를 평가해보자
> 이 평가는 다른 모델과의 비교에 있어 필수적임
> 그 모델의 성능 예측 가능
- expected value calculation
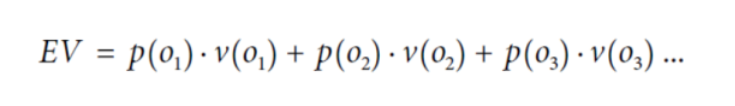
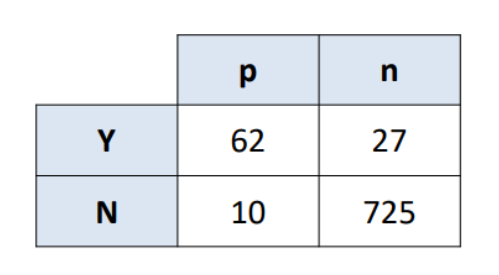
> 각 oi는 (Y, p), (Y, n), (N, p), (N, n)에 대응함 즉, 표에서 셀 한 칸에 대응되는 것
- Example
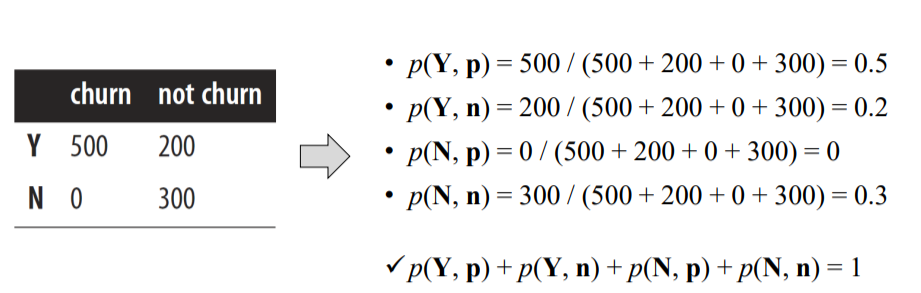
> 확률 값이기 때문에 다 더하면 1이 나옴
# Overview of the Expected Value Calculation
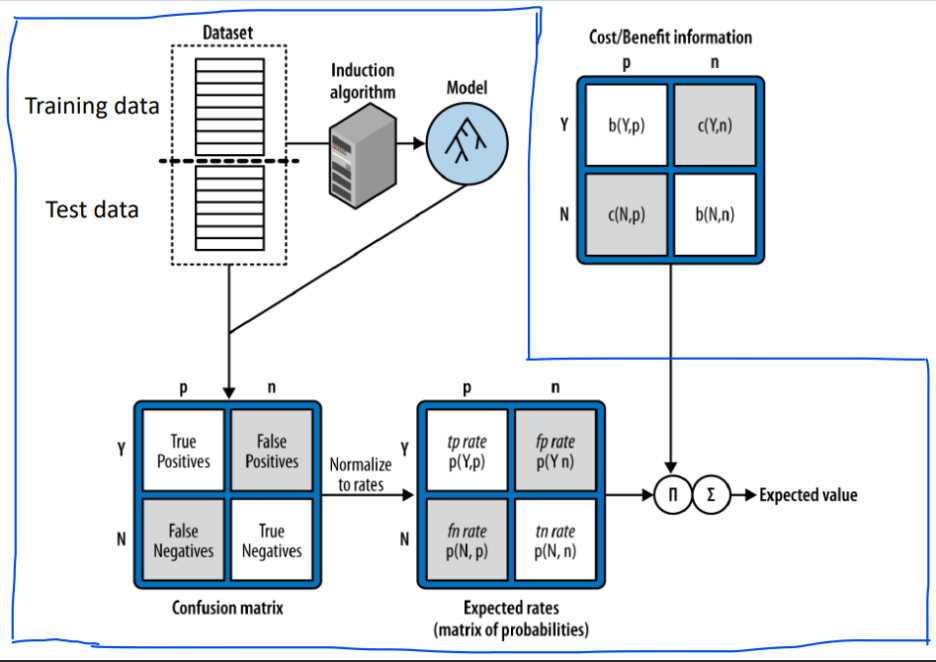
> 파란색 영역: 우리가 할 수 있는 영역
> Cost/Benefit information: 분석을 통해 외부의 정보 필요
> dataset이 있으면 training data, test data가 따로 있고
이것으로 모델을 만들면 confusion matrix를 만들 수 있음
> confusion matrix에서의 expected rates와
외부에서 얻은 정보를 통해 만든 cost/benefit information의 정보 값을 가지고
expected value를 만들 수 있음
# (Ex) Using EV for Classifier Evaluation
step1) Estimate the rate of each case
- 각 count를 전체 instance 개수로 나눈 것
- p(h, a): count(h, a)/T
> h: 예측 클래스 (Y or N)
> a: actual class (p or n)
> T: instance의 전체 개수
> count(h, a): 해당 case에 상응되는 instances의 개수
> p(h, a): 그 case의 비율(추정 확률)
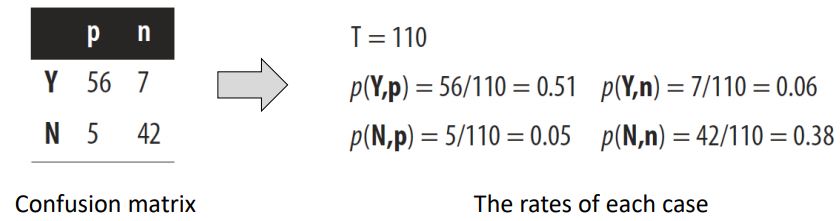
step 2) specify the value (cost or benefit) of each case
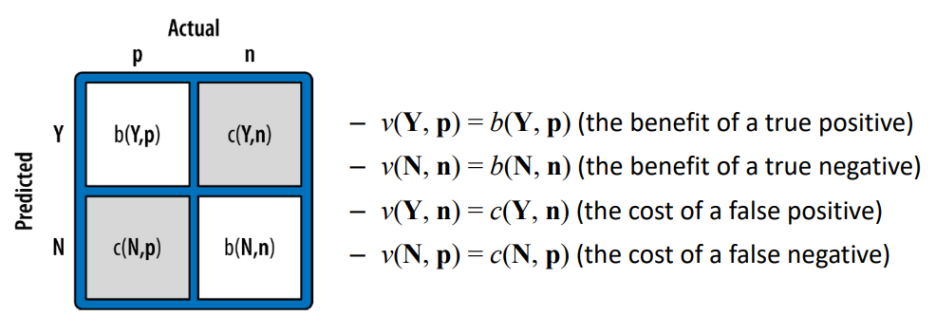
> b(h, a): benefit
> c(h, a): cost
- b(h, a)와 c(h, a)는 data로부터 추측할 수 없음
> 분석을 통해 제공되는 외부 정보에 의해 알 수 있는 것이 일반적
ex) 우표값이 $1라는 것은 data가 아닌 외부 정보로부터 결정되는 것
> 많은 시간과 생각이 필요한 부분임 / 그 고객을 붙잡는 것이 얼마나 가치 있는가?
Example) our targeted marketing example
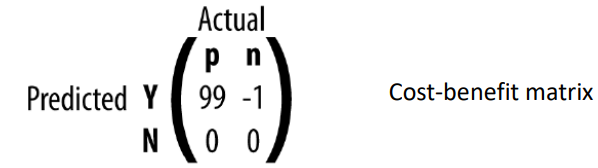
- v(Y, n): -1
> 살 사람이라고 예측해서 $1을 사용해 서비스를 제공했지만 사실 그 사람은 안 살 사람이었던 것
- v(N, p): 0
> 우리가 서비스를 제공했으면 살 사람이었는데 no라고 예측했기 때문에 서비스를 제공하지 않았음
> 이것을 살 사람이 안 사서 손해 봤다고 생각할 수 있지만, 여기 예시에서는 우표값 안 들고
그냥 소득이 없었던 것이라고만 생각해서 0이라고 쓴 것
다른 측면에서는 손해로 -100이라고 생각할 수도 있음 이건 회사나 도메인에 따라 다르게 생각할 수 있는
부분임
- v(Y, p): 99
> 200 - 100(상품 생산하는데 드는 비용) - 1 (우표 값) = 99
- v(N, n): 0
> 안 살 사람을 안 산다고 예측해서 아무 손실이 없음
step3) compute the total expected value (or profit)
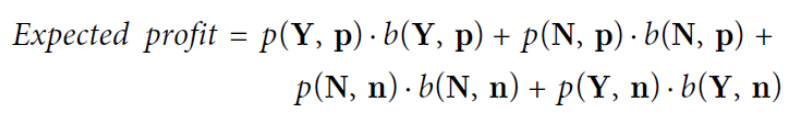
- model의 기대 이익을 계산하기 위해 위의 방정식을 사용
- total 기대 수익을 나타냄
# Alternative Calculation of EV
- EV 방식은 실제로는 잘 쓰이지 않음
- 조건부 확률의 개념을 도입하여 공식을 바꾸는데 이것이 데이터 사이언스에서 많이 사용됨
- 조건부 확률: A가 일어났을 때 발생하는 확률
- 조건부 확률 사용
> 사전 클래스 (Class priors): p(p), p(n) → 모델을 돌리기 전에 알고 있는 정보
> 조건부 확률: p( x, y) = p( y )* p( x | y ) → y가 주어졌다는 가정 하에 x가 일어날 확률
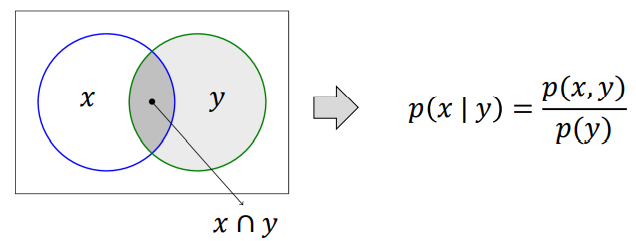
> p(x | y)는 x와 y가 동시에 일어날 확률을 y가 일어날 확률로 나눈 것임

> contribution: weight와 비슷
> p(p), p(n): positive/negative일 각각의 확률
- Example
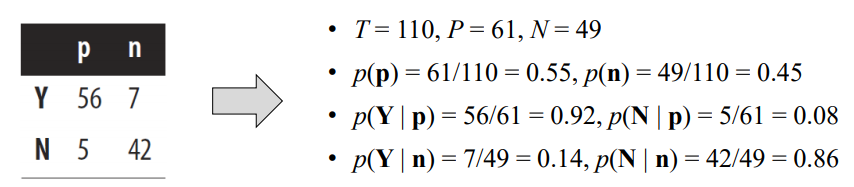
- calculate the total expected profit
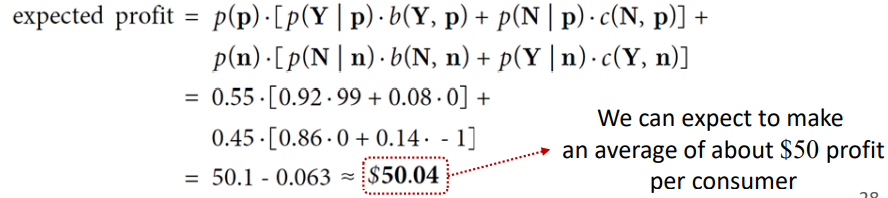
> average: expected value
- 정확도를 계산하기보다 기댓값을 계산해야 함
- 다양한 분포도에 대해 두 모델을 쉽게 비교할 수 있음
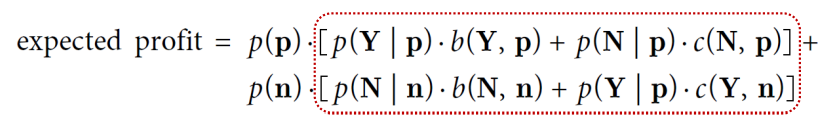
.
> 빨간 부분의 계산 결과는 달라지지 않음 → p(p)와 p(n)만 계산하면 되기 때문에 계산이 쉬워짐
* example
| p | n | |
| Y | 56 | 7 |
| N | 5 | 42 |
> 110개의 데이터를 기반으로 그린 matrix가 위와 같다고 하자
> p:n의 분포도가 바뀌어도 같은 row끼리의 합은 변하지 않음 Y: 63/ N: 47
> column의 비율은 변할 수 있음
> data가 달라지거나 수가 더 많거나 적어진다 해도 같은 모델이기 때문에
Yes/No로 분류되는 비율이 달라지지는 않음
# Other Evaluation Metrics
- data science에서 사용되는 평가 metric은 많음
> 모든 평가 metric은 confusion matrix를 근본적인 요약한 것임
- Accuracy : 내가 맞춘 것을 전체로 나눈 것
= (TP + TN)/(TP + FN + FP + TN)
- Sensitivity (True positive rate): 실제 positive 중 잘 맞춘(Yes라고 예측) 것의 비율
= TP / (TP + FN) = 1 - False negative rate
ex) 암 진단에서 의사가 100명의 암 환자 중 이들이 암 환자라고 제대로 진단할 비율
- False negative rate: 실제 positive 중 맞추지 못한 것(No라고 예측)의 비율
= FN / (TP + FN)
- Specificity (True negative rate): 실제 negative에서 잘 맞춘(No라고 예측) 것의 비율
= TN / (FP + TN) = 1 - False positive rate
- False positive rate: 실제 negative 중 맞추지 못한(Yes라고 예측) 것의 비율
= FP / (FP + TN)
- 주로 정보 검색이나 패턴 인식 (text classification)에서 사용되는 용어
> Precision: Yes라고 예측한 것 중에 실제 Positive인 것의 비율
= TP / (TP + FP)
> Recall: 민감도와 같지만 해당 분야에서는 이 이름으로 불림
= TP / (TP + FN)
> F-measure: 조화 평균
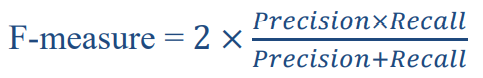
* 조화 평균: 어떤 값들이 있을 때, 그 값들에 역수의 평균의 역수
# Baseline Performance
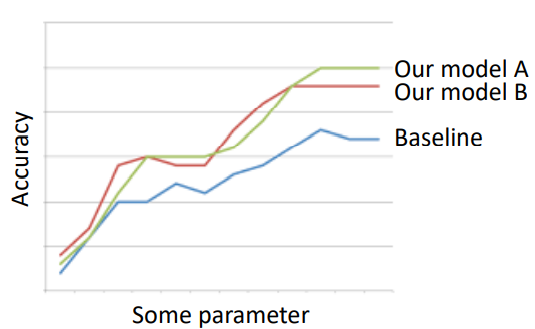
- 모델의 성능을 비교할 baseline을 우리의 model이 가지고 있음을 보여야 함
- 적절한 baseline
> 실제 적용에 따라 달라짐
> 매우 도움이 되는 일반적인 규칙들이 있음
# Baselines for Classification Models
① Random model
- 큰 의미가 있거나 값 어치가 있지 않음
- 모델에 대한 지식이 아무것도 없는 inital 상태에서 모델을 만들었을 때 또는 매우 어려운 문제에서 사용
- 적어도 만든 모델이 랜덤 모델보다는 성능이 좋아야 함
② simple (but not simplistic) model
- 너무 간단하지 않은(?) 간단한 모델임
- ex) 날씨 예보
> 내일 날씨는 오늘과 같을 것임
> 10년, 20년 전의 오늘 날짜의 평균 날씨
> 랜덤 모델보다는 나음
③ The majority classifier
- 다수결에 따름
# Baselines for Regression Model
- 평균값을 많이 사용 + 중간값
- 추천 시스템을 고려해보기
> 특정 영화에 대해 고객이 별점을 얼마나 줄 것인가
> simple model
→ model1: 고객이 영화에 주는 별점의 평균
→ model2: 영화가 고객에게 받는 별점의 평균
# Baselines for Other Tasks
- domain knowledge (received wisdom): 학습을 통해 알 수 있는 + domain을 통해 아는 지식
> domain knowledge를 기반으로 한 모델을 baseline model로 사용
- ex) Fraud detection
> 내 계정이 탈취당한 것을 감지하는 모델
> 랜덤보다 알 수 있는 domain을 이용해 baseline 설정 가능
> 안 쓰던 패턴(하루에 100-200만 원 소비)이 생기면 의심
'Study > Data Science' 카테고리의 다른 글
| [DataScience] Ch9. Evidence and Probabilites (0) | 2021.08.24 |
|---|---|
| [DataScience] Ch8. Visualizing Model Performance (0) | 2021.08.24 |
| [DataScience] Ch6. Similarity, Neighbors, and Clusters (0) | 2021.08.24 |
| [DataScience] Ch5. Overfitting and Its Avoidance (0) | 2021.08.24 |
| [DataScience] Ch4. Fitting a Model to Data (0) | 2021.08.23 |
