1. Ch4. Fitting a Model to Data
- 숙명여자대학교 소프트웨어학부 데이터사이언스개론 - 박동철 교수님
1.1. # Predictive Modeling
- 다른 attribute의 측면에서 target 변수의 model 찾기를 포함
- predictive modeling의 두 가지 유형
① Nonparametric modeling
> model의 구조가 고정되지 않음
> model의 구조는 data로부터 결정됨
> ex) tree → data에서 ig, 엔트로피를 통해서 정해짐
② Parametric modeling
> model의 구조가 고정됨
> model의 구조는 data 분석에 의해 명시됨
> ex) y = ax + b (a, b는 상수)
1.2. # 1. Nonparametric Modeling
- model의 구조를 명시할 수 없음
- model의 구조는 data로부터 학습됨
- Example: Classification tree induction
> tree의 구조는 data로부터 자동적으로 결정됨

1.3. # 2. Parametric Modeling
- parameter learning이라고도 함
- 기본적인 접근
① 특정 매개 변수를 지정하지 않고 모델의 형식을 지정
> ex) 매개 변수화 된 수학 함수
Y = a*X + b → a: attribute weight
② 주어진 training dataset에서 최상의 매개 변수를 찾음
> 가능한 model을 data에 fit시킬 수 있도록 매개변수를 조정해야 함 → fitting a model to data
Y = 1.39*X + 4.78 → 만든 모델
- Example: Linear regression

* 금 값 ↑ → 달러 ↓ = 부채 많아짐
- model의 형태는 Domain knowledge 혹은 다른 data mining techniques에 기반하여 선택됨
* data mining techniques ex) the informative attribute selection
- 목표
> model parameter의 최적의 값을 찾아야 함 → optimal
> 최적의 값을 찾는다는 의미가 model이 data에 잘 fit 되는 것을 의미하는가?
- Example: Linear regression
> 어떤 line이 best일까?

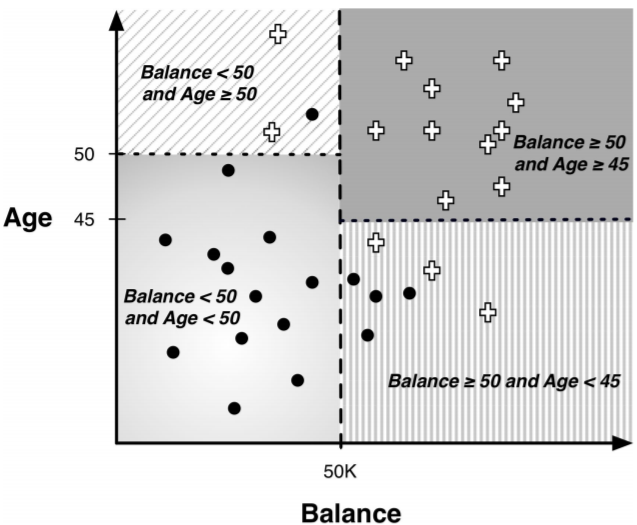
1.4. # The Space Partition of Classification Trees
- space는 decision boundaries에 의해 영역들로 쪼개짐
* 영역 = class, segmnet, decision boundary = 점선
- 새로운 instance가 segment에 포함되는 경우, instnace의 목표값을 segment의 목표값으로 결정함
1.5. # Another Way to Partition The Space
- 선이 축에 수직이 아닌 경우 → not perpendicualr to the axis
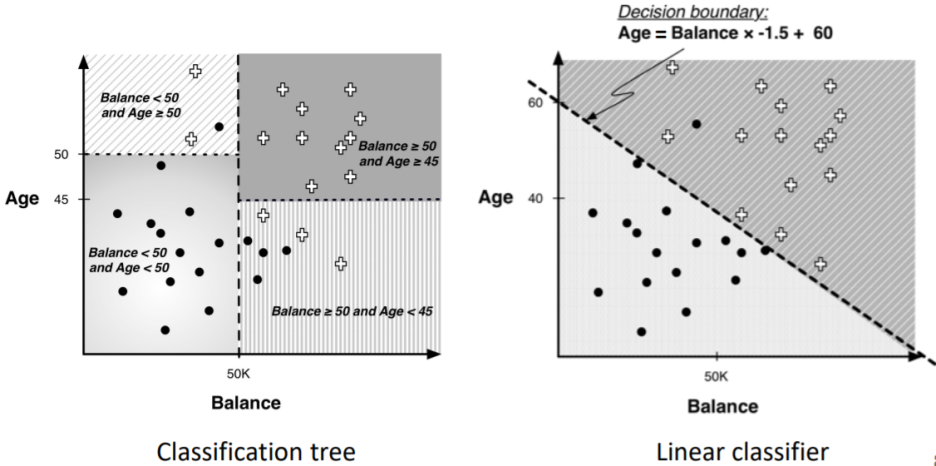
1.6. # Linear Classifier
- 속성의 linear combination을 사용해 space를 나눔
> linear combination: attribute 값의 weighted sum
y = ax + b (y: attribute, x: attribute)
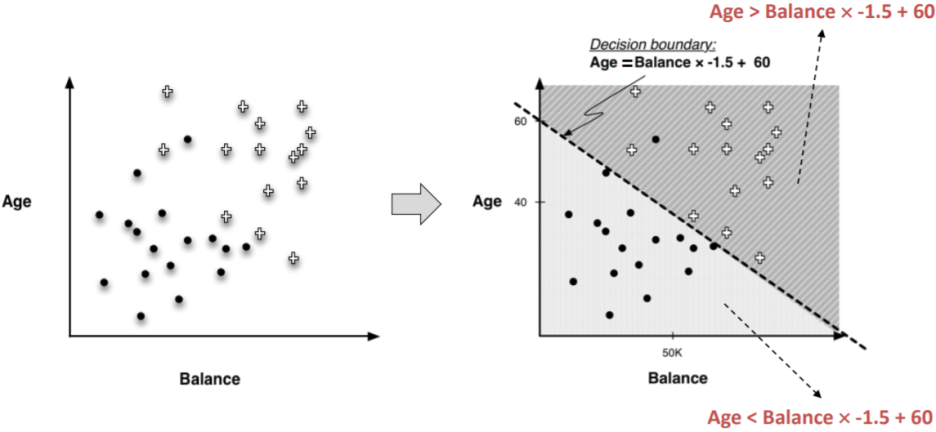
- Age의 wight: 1, Balance의 weight: -1.5 → 각 변수(속성 값)의 계수
1.7. # Classification Tree VS. Linear Classifier
- target 변수의 다른 값을 가지고 data를 영역으로 쪼갠다는 목표는 같음
- 형태는 다름
> Classification Tree

> Linear classifier

1.8. # General Linear Classifier
- 아래 주어진 data를 고려

X: unseen dataset
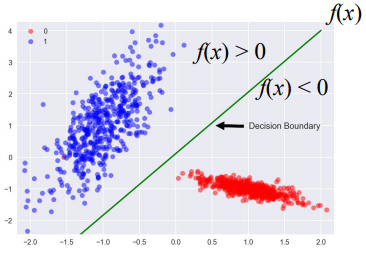
- x를 분류하기 위해 일반적인 linear classifier는 아래의 함수를 사용
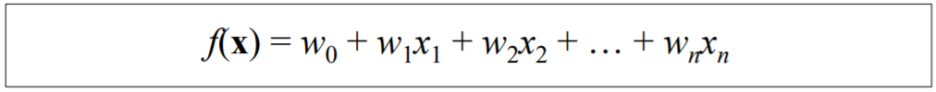
- w0: 상수
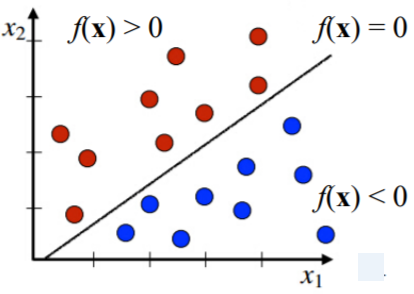
> 만약 f(x)>0이면, x는 "red"로 분류됨
> 만약 f(x)<0이면, x는 "blue"로 분류됨
> w0, w1, ... , wn: model의 parameter
= features' weights
1.9. # The Shape of Decision Boundary
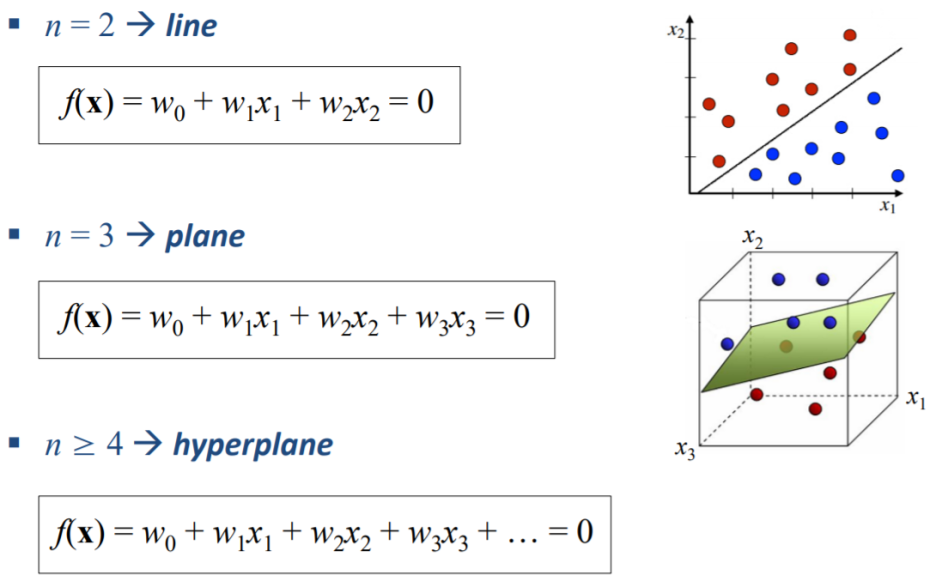
* n >= 4: 인간의 인지를 벗어남
1.10. # The Goal of General Linear Classifiers
- training dataset이 주어지면, w0, w1, ... , wn의 최적의 값을 찾음
> training data를 잘 분류하고 새로운 data를 가능한 정확하게 분류함
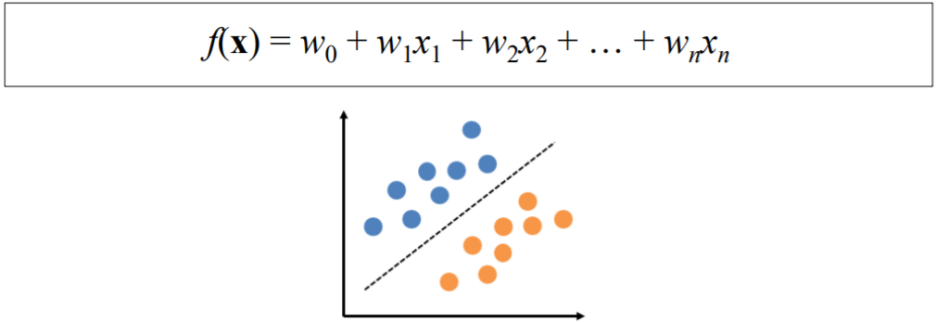
- wn: weight 값, Xn: attribute
- w0, w1, ... , wn에 대한 해석
> wi가 클수록 xi는 target을 분류하는데 중요성이 더 커짐
> wi가 0에 가까우면 xi를 무시하거나 버려도 됨
1.11. # Finding the "Best" Line
- class를 분류하기 위해 "best" line을 선택하는 것은 사소하지 않음 → not trivial
> 여러 개의 후보 line 중, 무엇을 선택해야 할 까?
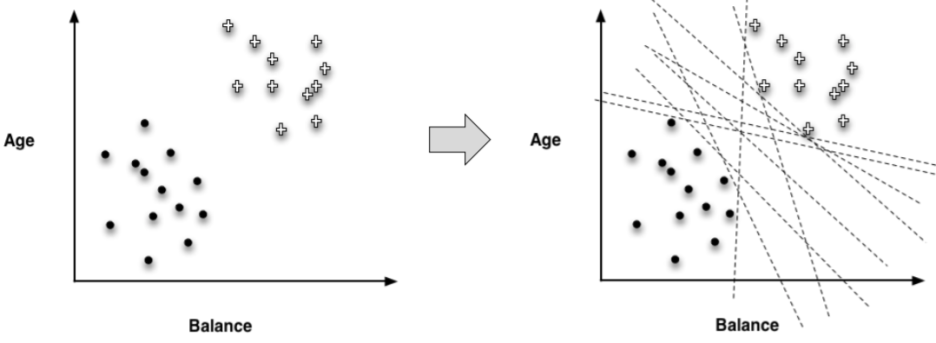
1.12. # What Weight Should We Choose?
- 일반적인 과정
① 우리의 목표를 나타내는 objective function을 정의
② objective function을 최대화 혹은 최소화하는 weight에 대해 극대화 값을 찾음
- 다음의 model들은 같은 형태를 가지지만, w0, w1, ... , wn의 best 값을 찾기 위해서 다른 objective 함수를 사용
→ 모델이 다름 * 모델: weight를 찾는 과정
> Support vector machine (SVM) (classification)
> Linear regression (regression)
> Logistic regression (classification)
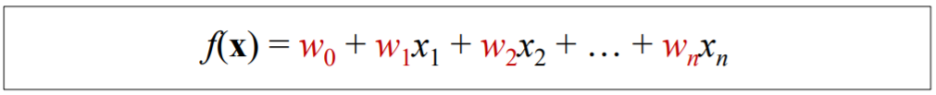
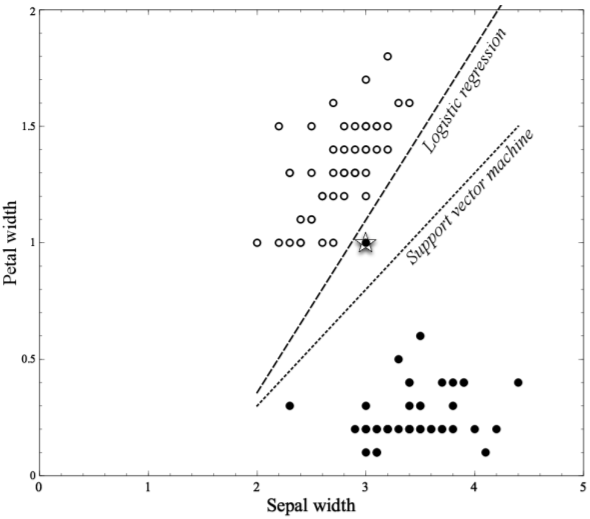
1.13. # EX) SVM VS. Logistic Regression
- 두 개의 classification 방법은 다른 boundary를 만듦
> 다른 objective function을 극대화하기 때문임 → 다른 objective function = weight가 다르다
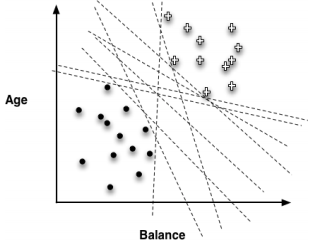
1.14. # Support Vector Machine (SVM)
- SVM은 linear classifier임
> SVM은 특징의 linear combination에 기반하여 instance들을 분류
> 새로운 데이터가 들어왔을 때 좀 더 명확하게 잘 분류할 수 있다는 가정하에 만듦
- 어떤 line이 SVM에서 가장 최적의 line일까?
→ SVM에서 data에 맞게 사용되는 objective function은 무엇인가?
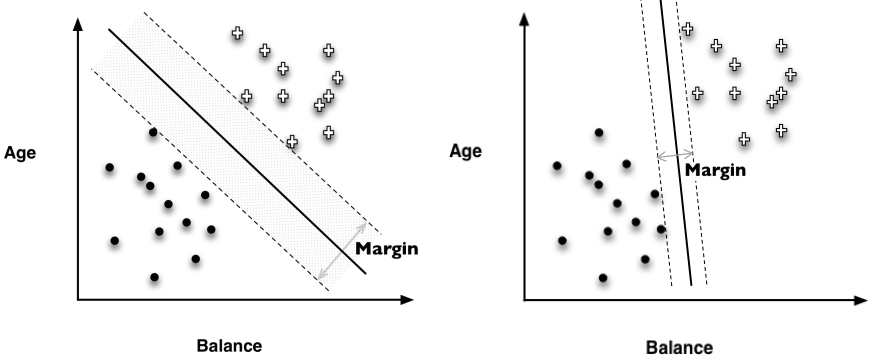
1.15. # The Basic Idea of SVM
- 가장 좋은 linear clasifier은 margin을 극대화하는 line임
> margin: 점선 사이의 거리
> 가운데 선이 SVM에서 사용되는 lienar classifier임
- 가장 좋은 line은 클래스들 모두에서 제일 먼 선임
1.16. # What About Misclassification?
- 단일 line이 data를 class들로 완벽하게 분리하지 못하는 상황이 있을 수 있음
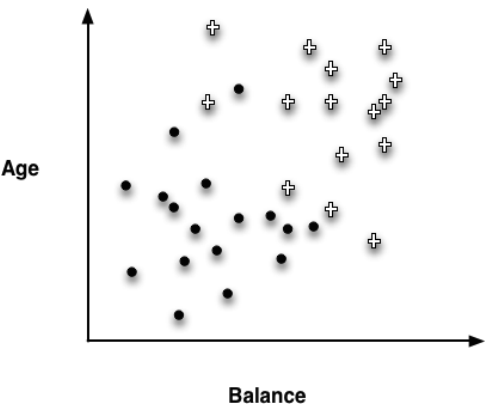
이 예시에서 data를 완벽하게 나눌 수 있는 선은 존재하지 않음
1.17. # SVM's Approach to Misclassification
- Main idea
> original objective function: line의 margin 크기를 측정
> New objective function: 각각의 training data에서의 instance가
misclassified 되는 것에 대해 penalty를 부여
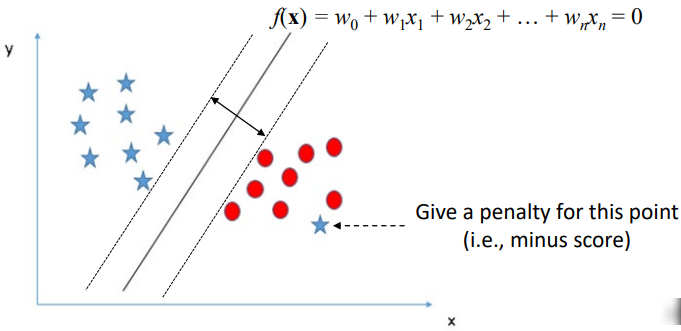
- penalty 부여 방법
> margin boundary에 따라 비율적으로 부여
> penalty의 유형은 hinge loss fuction이라고 불림 * hinge: 접히는 부분
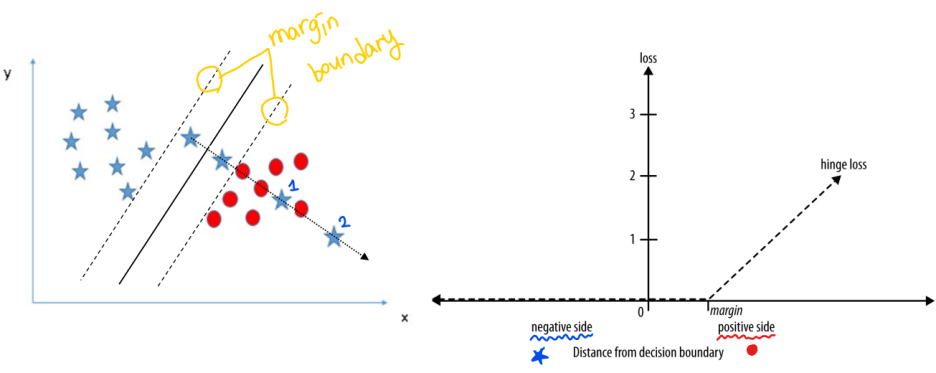
- margin boudary를 벗어난 ★ 1, 2에 대해서만 penalty 부여
> 이때, 1보다는 2에게 더 많은 penalty를 부여함
- 오른쪽 그래프에서 ★입장을 생각해보면
positive side를 지난 이후부터hinge loss가 커지는 것을 확인할 수 있음
1.18. # Linear Regression
- data를 잘 묘사하는 linear function을 찾음
> target attribute의 값을 예측하는 데 사용됨
- 어떤 line이 lienar regression에 가장 잘 맞는 line일까?
→ linear regression에서 사용되는 objective function은 무엇인가?
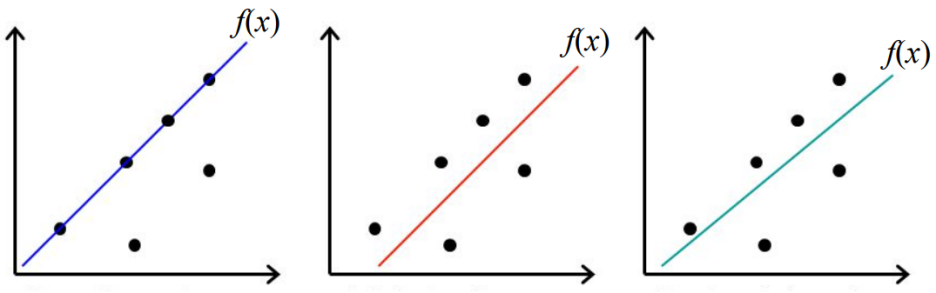
- 다른 objective function들을 사용하는 linear regression 과정이 있음
- 일반적인 linear regression의 과정
> training data에서 각 individaul point에 대한 error를 계산
* error는 point와 line의 거리임 (= absolute error)
> absolute error들을 더함
> error들의 합을 최소화하는 w0, w1, ... , wn을 찾음
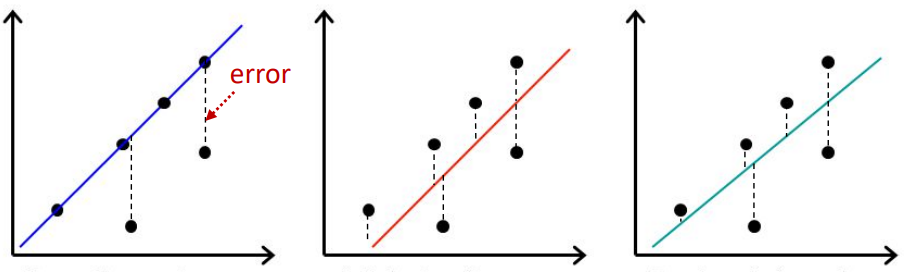
1.19. # Least Squares Regression
- 가장 common("standard")한 linear regression 과정
- objective function (least squares estimate의)
> error들의 제곱의 합을 최소화하는 w0, w1, ... , wn을 찾음
- "Squares"를 사용하는 이유?
> 만약 absolute errors의 합을 최소화한다고 할 때 아래의 예시들에서는 어느 하나를 고르기 어렵기 때문
→ 수학적으로 w0, w1, ... , wn값을 찾기 어려움
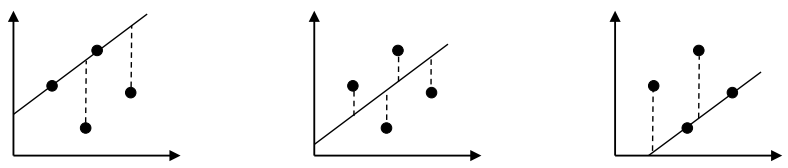
- 이점
> 제곱의 지수 값이 높을수록,outlier(특이치)'s error가 더 증폭됨
> 수학적으로 쉬움: 2차 함수의 최솟값을 찾는 것은 쉬움
- 2차 함수를 미분하고 도함수가 0이 되는 지점을 찾으면 됨
- 단점
> outlying data points로 인해 생긴 결과가 linear function을 심하게 왜곡할 수 있음
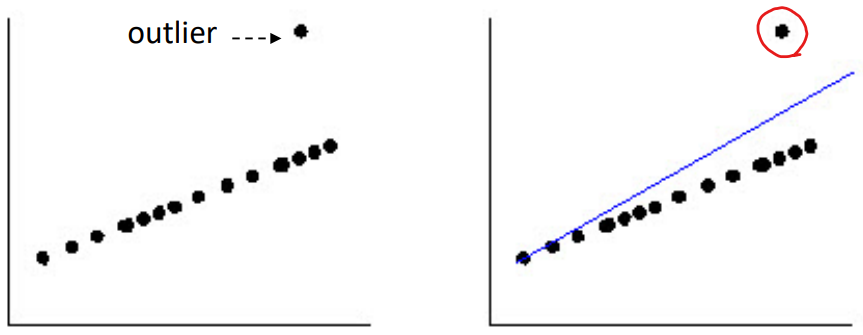
빨간 원의 영향이 너무 커서 weight가 달라짐
1.20. # Logistic Regression
- Logistic regression은 linear regression과 비슷함
> 두 개 모두 지도 학습 알고리즘임 → supervised machine learning algorithm
> 두 개 모두 자연스럽게 학습하기 때문에 이런 알고리즘은 예측하기 위해 label 된 data를 사용함
> Linear Regression은 regression 문제를 풀기 위해 사용되고
Logistic Regression은 classification 문제를 해결하기 위해 사용됨
- 언제 logistic regression을 사용할까?
> 두 개로 나눠지는 분류를 가지는 interest의 결과와 독립적이지 않은 변수의 수가 있을 때
→ binary outcome(=categorical depentdent variable) * binary: 0과 1처럼 두 개로 나누어지는 분류
y = ax + b
> y는 a, x, b에 의존적이고 a, x, b는 독립적임
> x = attribute
- Examples of binary outcome
> Gaming(win/loss), sales(buying, not buying), credit card or loan(default/ non default), healthcare(cure, non cure), marketing(response, no response), etc..
- 새로운 instance가 interest의 class에 속할 확률을 추정하기 위해 lienar model f(x)를 사용
* f(x): linear classifier가 사용하는 fucntion
> ex) f(x) =0.85 → x가 특정 class에 속할 확률은 0.85 임
- f(x)를 x의 class 확률을 추정하는데 바로 사용할 수 있나?
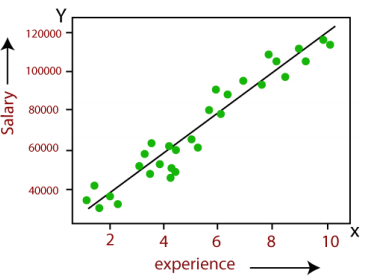
> No
> f(x)의 범위는 (-∞,∞)이고 확률의 범위는 0부터 1까지이므로 범위가 일치하지 않기 때문
- 우리는 0과 1 사이의 확률을 예측하는 model을 원함
> linear regression은 맞지 않음
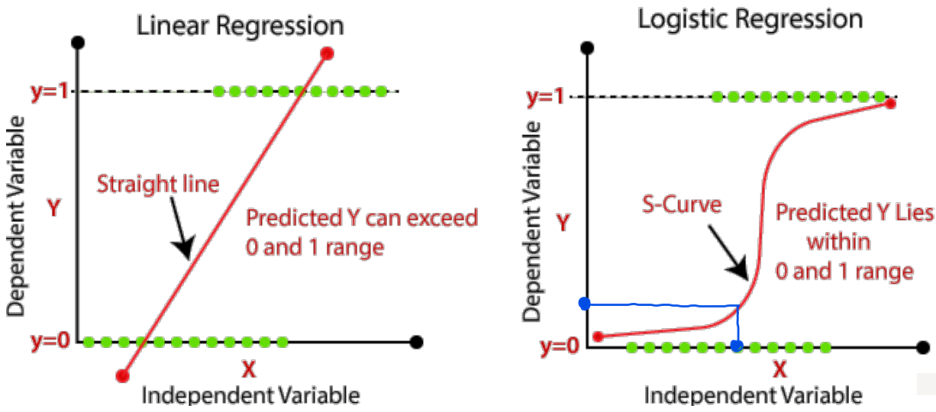
.
- logistic regression은 classification 문제를 해결하는 것이지만
위의 그림과 같이 x에 따라 y가 정해 지므로 이름에 regression이 붙게 되었음
- logistic regression을 위해 f(x)에 대해 공식 변형이 필요
- Logistic function p(x) → Standard임
> S모양의 커브는 아래의 방정식에 의해 만들 수 있음
> x의 class 확률을 추정할 때 사용됨
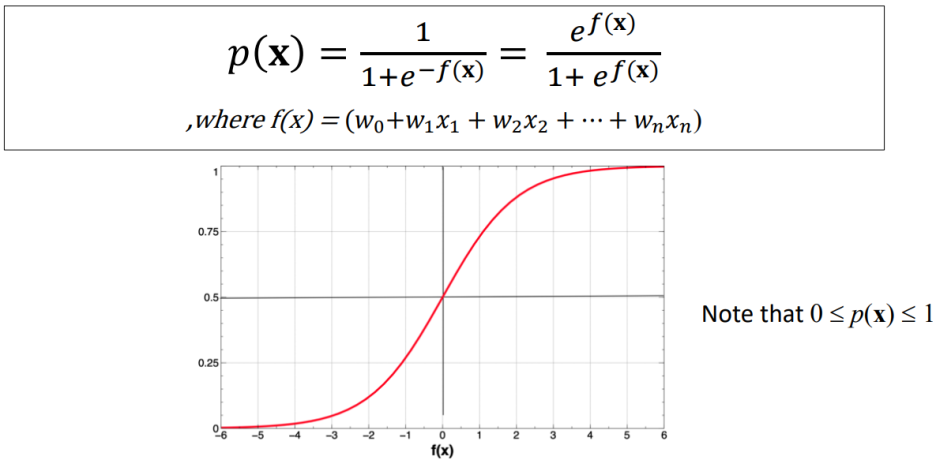
- p(x)는 f(x)의 값을 0과 1 사이 값으로 변형시킴
- Logistic Regression의 정의: linear regression logit으로 변형하는 것
① odds(승산): 사건이 일어날 비율에 대한 사건이 일어나지 않을 비율의 비 // p/(1-p)
ex) p: 0.5 → odds = 1 / 0.5/0.5
② Log odds (Logit): odds에 자연로그를 씌운 것 // ln(p/(1-p))
③ 우리는 Log odds로부터 class membership의 확률을 추정하기를 원함

④ logistic regression의 방정식
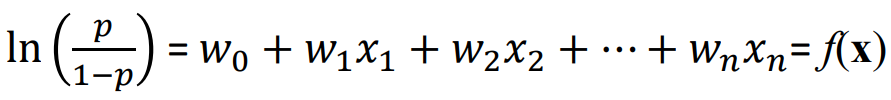
1.21. # Objective Function for Logistic Regression
- Maximum likelihood model
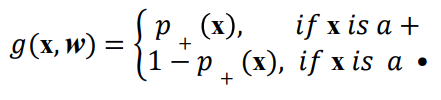
> 가능성 = 확률 값
> p(x)가 달라지면 g(x, w)도 달라짐 → weight 값에 따라 g값도 달라짐
> x: attribute, w: 우리가 찾고자 하는 w0, w1, ... , wn의 vector 값
- g 함수는 x의 특징이 주어진 x의 실제 class를 볼 수 있는 model의 추정된 확률을 알려줌
- label 된 datasets의 모든 예를 통틀어 g 값을 합하는 것을 고려하고
이것을 다른 parametered 된 model에도 적용함
→ in our case, logistic regression에 대한 다른 wieghts의 집합임
- 가장 큰 합을 제공하는 model이 data에 대해 높은 가능성을 제공하는 model임 (maximum likehood)
- 일반적인 경우에서 Maximum likelihood model은 positive 예에 대해 가장 높은 확률을 주고,
negative 예에 대해서는 낮은 확률을 줌
1.22. # Using a Logistic Regression Model
- p(x)를 training data로부터 만들어진 logistic regression model이라고 하자
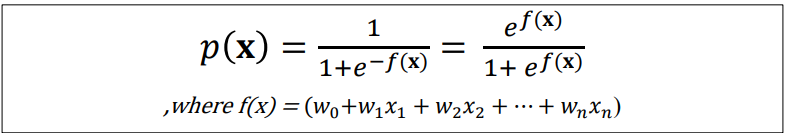
- x = (x0, x1, ... , xn)이고 이는 새롭고 본적 없는 instance임
- 만약 p(x) > 0.5 라면, 우리는 x를 positive(+)라고 결정함
> p(x) > 0.5는 f(x) > 0 과 같음
- 만약 p(x) < 0.5 라면, 우리는 x를 negative(-)라고 결정함
> p(x) < 0.5 는 f(x) <0과 같음
1.23. # Linear regression VS. Logistic regression
| Linear Regression | Logistic Regression |
| 주어진 독립적 변수의 집합을 사용해 연속되고 의존적인 변수를 예측하는데 사용됨 (Regression problem) | 주어진 독립적 변수의 집합을 사용해 categorical 의존 변수를 예측하는데 사용됨 (Classification problem) |
| 값, 나이 등과 같은 연속적인 변수의 값을 예측함 | Yes or No, 0 or 1과 같은 categorical 변수의 값을 예측함 |
| output을 쉽게 예상함으로써, 가장 잘 맞는 line을 찾음 | sample을 분류함으로써 S-curve를 찾음 |
| 정확도를 측정하는데에 Least squares estimation method가 사용됨 | 정확도를 측정하는데에 Maximum likelihood estimation method가 사용됨 |
| 의존적 변수와 독립적 변수 사이의 관계가 linear해야 한다는 것이 요구됨 | 의존적 변수 그리고 독립적 변수 사이의 관계가 linear해야 한다는 것을 요구하지 않음 |
1.24. # Classification Trees VS. Linear Classifiers
- 두 개 모두 predict, classification model을 푸는 것임
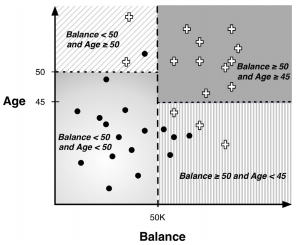
- Classification tree
> overfitting 문제
> instance 공간의 축에 수직인 decision boundary를 사용
> instance 공간을 많은 작은 영역으로 나눔
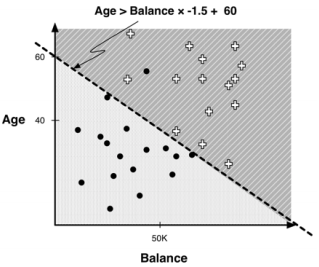
- Linear classifier
> decision boundary를 어느 방향으로 사용할 수 있음
> instance 공간을 두 개의 segment로 나눔
1.25. # Which One Is Better?
- 미리 결정하는 게 어려움
> 가장 좋은 decision boudary가 어떻게 보일 것인지 모르기 때문
→ target 변수의 다른 값을 가지고 data를 영역으로 쪼개기 때문에 어떻게 될지 모름
- 이해에 있어 차이가 있음 → comprehensibility = understandability
> Logistic regression: 통계학자가 아닌 사람들에게 설명하기 힘듦
> Decision tree: 대부분의 사람들에게 더 이해가 잘 되게 설명할 수 있음
- 위의 문제가 왜 중요한지?
> 대부분 이해관계자들에게 model을 설명할 때 그들이 이해해서 만족해야 하기 때문
1.26. # Example: Logistic Regression
- Wisconsin 주의 유방암 dataset
> 각 예시는 사진의 세포핵의 특성을 묘사함
> 양성 혹은 악성(암)으로 label 됨 → benign or malignant
> 이미지의 수: 376(양성) + 212(악성)
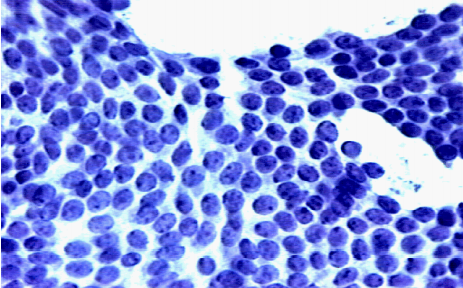
- Wisconsin 주의 유방암 dataset의 attribute
> digitized 된 사진으로부터 계산됨
> 사진에서 세포핵 모습의 특성을 묘사
- logistic regression에 의해 학습된 Linear 방정식

- logistic regression model의 정확성
> 98.8% (6 mistakes / 588 images)
- 같은 dataset으로부터 학습된 classification tree
> 정확성: 99.1%
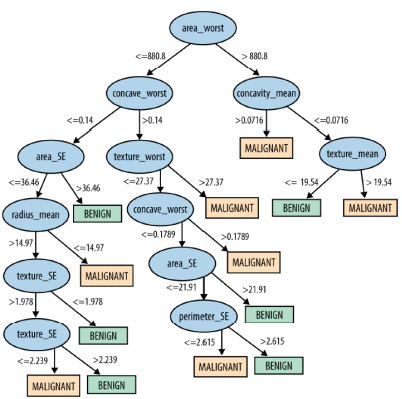
- 질문 1: 98.8%의 정확성은 좋은 결과인가?
> data mining에서 그 정도의 정확성은 흔하게 볼 수 있음
> 실제로 classifiers를 평가하는 것은 어렵고 복잡함
- 질문 2: classification tree는 더 좋은 model인가?
> logistic regression model와 classification tree의 차이는 mistake 1개로 인한 오류로 야기되었음
> 정확도의 숫자는 각 모델을 구축할 때와 같은 dataset에 대해 평가함으로써 이끌어냄
1.27. # Linear Classifier for Ranking Instances
- instance가 class에 속하는지 여부를 단순히 yes or no로 단순하게 예측하는 것을 원하지 않음
- 한 클래스 또는 다른 클래스에 속할 가능성에 의해 instnace를 서열화하기 원함 → ranking
> 이 customer가 우리의 제안에 반응할까? → Yes/No
> 어떤(특징을 가진) customer들이 우리의 제안에 반응을 잘할까? → ranking
- Linear classifier에서 ranking을 위해 따로 할 일은 없음
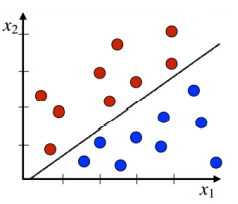
- Observations
> decision boundary에 가까움: 우리는 클래스에 속할 확률이 불확실하다고 생각함 → f(x)가 0과 비슷함
> decision boundary에서 멈: 클래스에 속할 높은 가능성을 가짐 → f(x) >>0
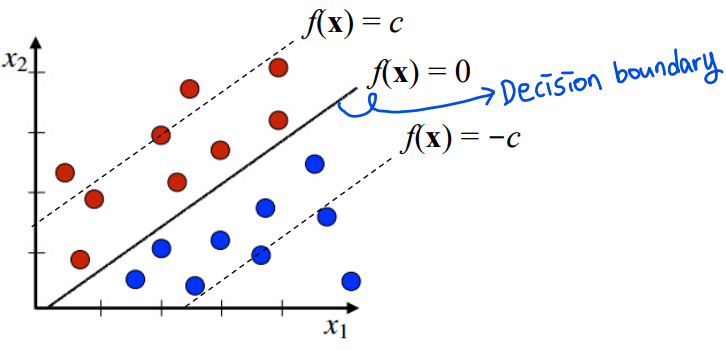
- Conclusion
> f(x) 자체를 사용하여 interest 클래스에 속할 가능성에 의해 직관적으로 만족스러운 인스턴스 서열을 얻음
1.28. # Nonlinear Models
- linear model: separate the data with a straight line
- Nonlinear model: separate the data with a curved line
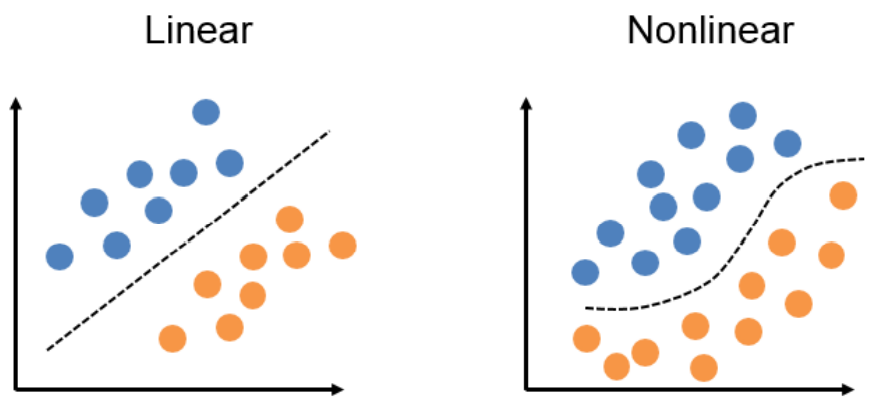
- linear model에 nonlinear 한 항들이 추가됨
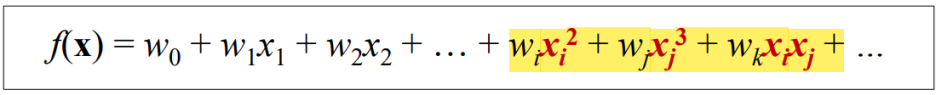
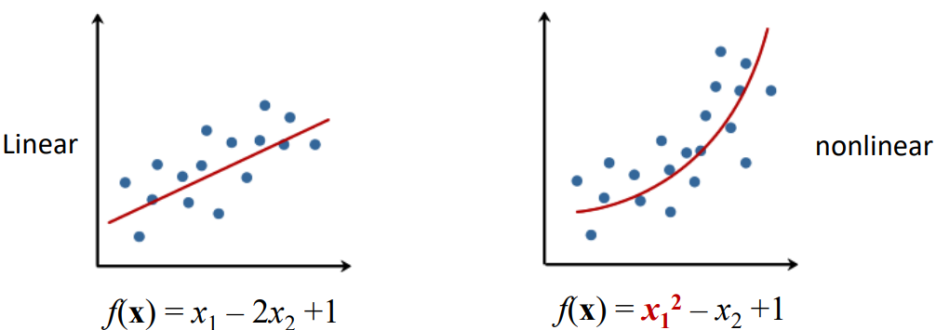
> linear term: 단 하나의 특징에 상수를 곱한 것만을 포함
> nonlinear term: 특징의 곱, 나눗셈, 지수화 또는 로그를 포함
- Logistic regression and SVM with a nonlinear term
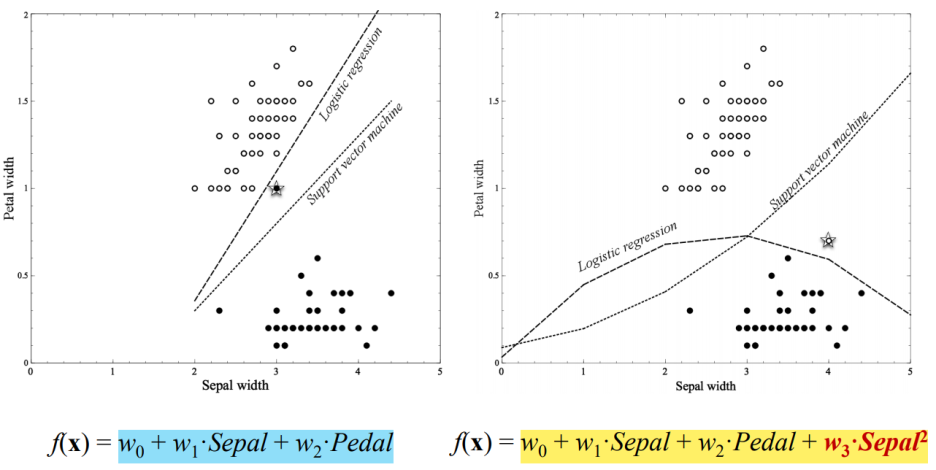
> 파란색 : lienar
> 노란색 : nonlinear
1.29. # Examples of Nonlinear Models
- Artificial neural networks → deep learning
> complex nonlinear function를 학습하는 데 사용됨
> 더 복잡한 function을 만들기 위해 많은 nonlinear function을 연결함
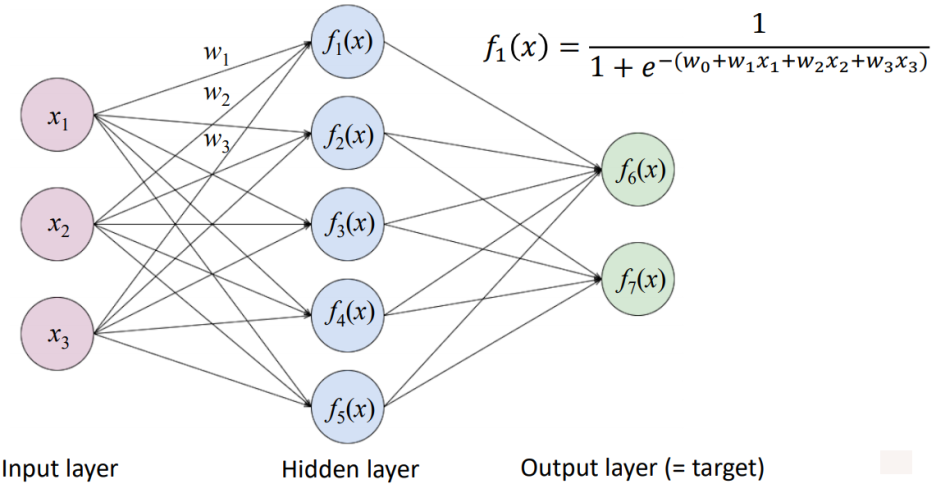
w: optimal 한 weight 값
1.30. # Logistic regression VS. neural network
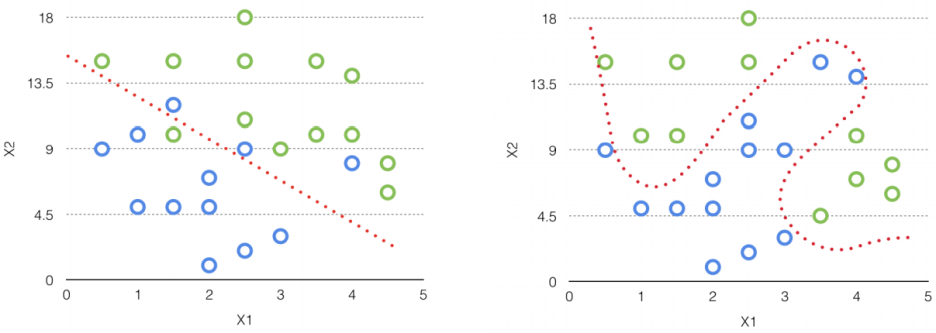
- Logistic regression: use a linear decision boudnary
- Neural network: use a nonlinear decision boundary
1.31. # Why Wouldn't We Do That All Time?
- tradeoff = overfitting
- 데이터에 너무 잘 맞으면 다른 dataset을 넣었을 때 일반화하지 못한다는 문제가 생김
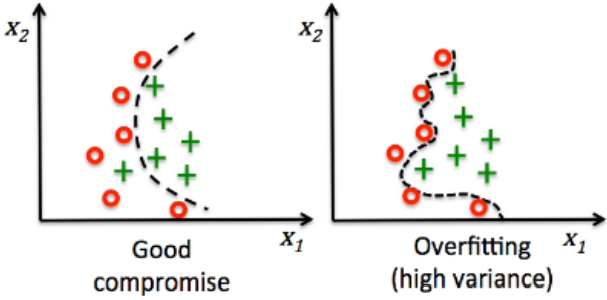
- 우리는 training datset을 넘어 다른 data에도 적용할 수 있는 model을 원함
1.32. # Summary
- Model fitting (or parametric modeling)
> The model is a partially specified numeric function, with some unspecified numeric parameters
> We "fit" the model to the data by finding the best parameters
> The meaning of "best" can be different for different ap plications → best = optimal
- Non-parametric modeling ex) classification tree
> not fix model
> The structure of a model is determined from data
- Learning modeling
> The form of the model: a simple weighted sum of attributes
> Includes support vetor machine, linear regression, logistic regression
> The difference is "What exactly do we mean by best fitting the data?"
① Support vector machine: a line that maximizes the margin
② Linear regression: a line that minimizes the sum of the squares of errors
③ Logistic regression: a line that maximizes the likelihood of class probability
'Study > Data Science' 카테고리의 다른 글
| [DataScience] Ch6. Similarity, Neighbors, and Clusters (0) | 2021.08.24 |
|---|---|
| [DataScience] Ch5. Overfitting and Its Avoidance (0) | 2021.08.24 |
| [DataScience] Ch.3 Introduction to Predictive Modeling: From Correlation to Supervised Segmentation (0) | 2021.08.23 |
| [DataScience] Ch.2 Business Problems and Data Science Solutions (0) | 2021.08.23 |
| [DataScience] Ch1. Data-Analytic Thinking (0) | 2021.08.23 |

