Ch3. Introduction to Predictive Modeling: From Correlation to Supervised Segmentation
- 숙명여자대학교 소프트웨어학부 데이터사이언스개론 - 박동철 교수님
* Modeling: 새로운 데이터가 들어왔을 때 결과를 예측하기 위함
# Predictive Modeling
- 일반적인 과정
> data를 잘 묘사하는 model을 구축 → Bulid a model
> 새로운 data의 결과를 예측하기 위해 model을 적용시킴 → Apply the model
- 첫 번째로 classification을 고려할 수 있음
> training data를 기반으로 새로운 data가 속할 class를 식별
# Model
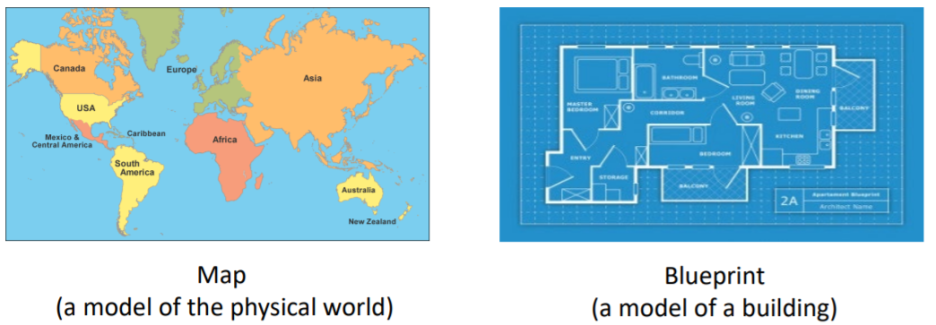
- 목적에 맞는 현실의 단순화 표현 → simplified representation
> 중요한 것과 중요하지 않은 것에 기초하여 단순화됨 → 목적에 맞지 않음 = 중요하지 않으므로 날려버림
> 관련 없는 정보는 추상화하고 관련 있는 정보는 보전함으로써 관련 없는 정보를 날려버림
# Types of Model: Predictive Model
- interest, 즉 target의 알려지지 않은 값을 추정하는 공식 ex) classification, regression
- The types of the formula

> Mathematical expression
ex) linear regression
> Logical statements (or rules)
ex) decision tree
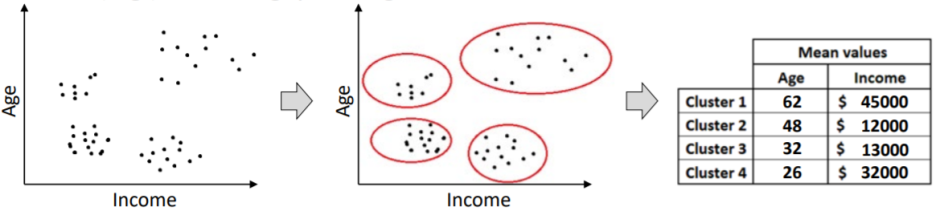
# Type of Model: Descriptive Model
- 주요 목적은 근본적인 데이터에서 insight를 얻는 것
ex) clustering, profiling → Unsupervised
- 수행에서 중요한 것
> Predictive model: 예측 정확도
> Descriptive model: 알려지지 않은 insight를 가지고 지식과 이해도를 높이는 것
- 많은 model들은 두 가지 다 고려할 수 있음
# Terminology (용어)

- target attribute
> 관심 있는 속성
- instance (or example, row)
> 사실 또는 data point를 나타냄
> 속성의 집합에 의해 묘사됨 ex) feature vector
- Model
> 특정 값이 주어지면 target의 값을 반환하는 함수
- Label (or class label)
> training dataset 안에 있는 target 속성의 값 ex) yes 또는 no
# Model Induction
- 데이터로부터 model을 생성. 즉, 특정 사례에서 일반적인 규칙으로 일반화함
- model은 통계적 감각 안에 있는 일반적인 규칙임 → 100% 발견되는 것은 아님
- 조건 (terms)
> Induction algorithm (or learner) → 유도 알고리즘 (학습자)
- data로부터 모델을 만드는 과정
> Training data (also called labeled data)
- model을 유도하는 데 사용되는 유도 알고리즘에 대한 input data
# Supervised Segmentation = classify
- 기본적인 idea
> 데이터를 target에 대한 다른 값을 가지는 하위 그룹으로 분할함
- 하위 그룹 내에서, instance들은 target에 대해 비슷한 값을 가짐
> 변수의 값을 사용하여 분할을 끝내면, target의 값을 예측하기 위해 변수의 값을 사용할 수 있음

기준: gender → 다른 기준이 있을 수 O
# Selecting Information Attributes
- 정보를 제공하는 방식으로 data를 분할하기 위해, 중요한 정보를 가지고 있는 속성을 사용
→ informative attribute
- Informative attribute
> target 변수에 대한 중요한 정보를 포함하고 있는 속성 / important information → 객관화/수치화 가능
> target 변수를 예측하는 것을 도와줌

- ex) 아래 사람들을 yes 혹은 no로 분류하고 싶음

> 속성
- 머리 모양: 사각형 혹은 원
- 몸 형태: 직사각형 혹은 타원
- 몸 색상: 검은색 혹은 하얀색
> target 변수: yes or no
> 분할에 있어 가장 좋은 속성: 가능한 만들어진 subgroup내의 값들이 pure 해야 함
> pure
- target 입장에서 group이 균일할 때 → homogeneous
- target 변수에 대해 group의 모든 member가 같은 값을 가지면 그 group은 pure 함
- 적어도 한 member라도 다른 값을 가지면 그 group은 impure 함

# Selecting Attributes to Segment Data
- 목표: 분할의 불순도를 최대한 줄이는 속성을 찾는다 → reduce the impurity of segments

# Complications (문제)
1. 속성을 완벽하게 group으로 나눌 수 없음

어떻게 나누는 게 더 나을까?
2. 모든 속성이 2개 중 하나의 값을 가지는 것은 아님 → Not binary
- 많은 속성들이 3개 혹은 더 구별되는 값을 가짐. 이때 어떻게 비교해야 하는가?
3. 숫자적인(or 연속적인) 속성을 사용하는 data는 어떻게 나누어야 하는가?
→ numerical attributes(continuous value)

# Splitting Criterion
- 각 속성이 데이터를 세그먼트로 얼마나 잘 분할하는지 평가하기 위해 공식을 만듦
> 그런 공식은 순도 척도에 기반을 둠 → based on a purity measure
- Information gain
> 기준을 나누는 가장 흔한 방법
> 순도를 측정하는 무질서도를 기반으로 함 → based on entropy

# Entropy
- 무질서도의 척도
> segment가 target 입장에서 얼마나 불순한가?

- Entropy 방정식

> H(s): segment S의 entropy
> pi: S에서의 class i의 비율
> ex) S = {Yes, Yes, Yes, No, No}
p1(Yes) = 3/5, p2(No) = 2/5
H(S)= 3/5*log2(5/3) + 2/5*log2(5/2) = 0.97
# Intuitive Understanding of Entropy
- entropy에 대한 직관적인 이해
- entropy H(S)의 구성
> p(+)와 p(-)가 각각 S에서의 +와 -의 백분율이 되도록 함

- 관찰
> H(S)는 calss들이 균형을 이룰 때 극대화됨 → p(+) = p(-) = 0.5
> H(S)는 모든 instance들이 + 또는 -일 때 최소화됨 → p(+) = 0 or 1
# Information Gain
* information gain 값이 높은 attribute를 선택!
- attribute를 선택할 때 data는 몇몇 segment로 나눠진다

- Entropy: 해당 segment가 얼마만큼 무질서하냐에 대한 것 → 전체를 보지 못함
> 각 segment가 얼마나 불순한지에 대해서만 알려줌
- Information gain
> 속성이 생성하는 전체 분할에 대해 entropy를 얼마나 향상할 수 있을지를 측정
- entropy가 감소되면, 우리는 정보를 얻음
- entropy가 증가되면, 우리는 정보를 잃음
# Definition of Information Gain
- 방정식

> IG: parent가 children c1, c2로 나뉠 대의 information gain → 높을수록 좋음
> 각 child ci에 대한 entropy는 그 child가 속하는 instance의 비율로 측정됨

parent: 100, c1: 70, c2: 30
c1's weight: 7/10, c2's weight: 3/10
- ex1) balance attribute에 기반을 두고 data를 나눔

- ex2) Residence attribute에 기반을 두고 data를 나눔

=> ex1과 ex2를 통해 알 수 있는 점:
balance를 속성으로 했을 때가 residence를 속성으로 했을 때 보다
IG가 더 높으므로 balance 속성이 더 유익하다
# Numerical Variables
- 속성이 숫자인 경우 ex) 회귀 문제
> category가 있는 속성에 기반하여 데이터를 분할하는 것은 쉬움
ex) Residence → OWN, RENT, OTHER
> 속성이 숫자인 경우 우리는 어떻게 데이터를 분할해야 하는가?
- Basic idea (1)
> 하나 혹은 그 이상의 분기점을 선택해 숫자 값을 이산화 시킴 → Discretize
> category가 있는 속성처럼 결과를 다룸

- Basic idea (2)
> 후보 분기점의 숫자를 선택함 → number of candidate split points
> 각 후보 분기점에 대해 information gain을 계산함

여기서는 후보 분기점이 35K 일 때 가장 높은 information gain을 얻을 수 있었음
# Tree-Structured Segmentation
- 지금까지 우리는 데이터를 가장 잘 분할할 수 있는 정보 속성을 찾는 것에 대해 이야기함
- 다중 속성을 사용하여 데이터를 분할할 수 있는가?
- 우리는 'tree' 형태로 데이터를 분할할 수 있음

# Classification Tree (Decision Tree)

- 구조
> interior node: 속성의 test를 포함함 → referred to as decision node
> leaf (terminal) node: 분할과 그것의 분류를 나타냄
> branch: 속성의 구별된 값 (또는 값의 범위)를 나타냄
> path from the root to a leaf: 분할의 특성을 알려줌
- 기본적인 과정
ex) 예를 들어 우리가 그것의 분류가 주어진 것을 알지 못한다고 할 때
> 예시에서의 특정한 값에 기반을 한 branch를 선택하며,
root node (starting)에서 시작하고 interior node를 따라 내려옴
> terminal node에 도착하면 그것은 분류를 줄 것임
- 예시: 이 고객이 채무가 필요한 상황임. 이 고객은 돈을 잘 갚을 것인가?를 예측하는 상황

> 그 사람을 Employed = No, Balance = 115K, Age = 40이라고 분류함
> root node에서 시작해 빨간 길을 따라 움직임
> 도착한 leaf node는 class = Not Write-Off라고 지정하고 있음
> 따라서 우리는 이 사람이 채무 불이행을 하지 않을 것이라고 예측할 수 있음 → Not default
# Creating Classification Tree
- tree induction: data로부터 classification tree를 만드는 것
- divide-and-conquer 접근
> 전체 dataset을 분할하기 위해 가장 적합한 attribute를 찾음
→ attribute는 information gain을 통해 얻을 수 있음
> 각 하위 그룹에 대해, 반복적으로 그 하위 그룹을 분할하기 위해 가장 적합한 속성을 찾음 → recursively

# Classification Tree Induction
- 아래 dataset을 고려해보자

> 속성
- 머리 모양: 정사각형 or 원
- 몸 형태: 직사각형 or 타원
- 몸 색상: 검은색 or 하얀색
> target attribute: Yes or No
> 첫 번째, 전체 dataset을 몸 형태를 기반으로 분할함
- 몸 형태가 가장 큰 information gain을 만들기 때문

> 두 번째, 직사각형이 몸의 형태인 그룹을 몸 색상에 기반하여 분할함
- 몸의 색상이 body shape의 하위 그룹인 직사각형 모양에 대해 가장 큰 information gain을 만들기 때문

> 마지막으로, 타원 모양의 몸 형태를 가진 그룹을 머리 모양에 기반하여 분할함
- 머리 모양이 몸 형태의 하위 그룹인 타원 모양에 대해 가장 큰 information gain을 만들기 때문

> Final classification tree

- Summary of tree induction process
> 반복적으로 데이터를 쪼개 나감
> 각 단계에서 모든 속성을 test하고 가장 pure 한 하위
그룹을 만드는 속성을 선택하여 분할할 속성을 선택함
→ information gain↑, entropy ↓
- when do we stop?
> 모든 leaf node가 pure 함
> 더 이상 쪼갤 변수가 없음
→ 검사에 사용할 attribute가 더 이상 없음
> overfitting 때문에 더 일찍 과정을 멈출 수도 있음
→ overfitting: 성능을 낮춤
# Visualizing Segmentations
- tree는 시작적으로 눈에 잘 들어오지 않기 때문에 이를 시각화하는 과정이 필요
- visualizing segmentation은 classification tree가 instance의 영역을
어떻게 나누는지 시각화하는데 도움이 됨

- 시각화는 오직 2개 혹은 3개의 특징에 대해서만 가능
- 하지만 이것은 higher dimensional에 적용하기 위한 insight을 제공함
# Trees as Sets of Rules
- classificaion tree는 해석하기 쉽기 때문에 대중적임
> 매우 복잡한 수학적 공식이 아님
- 논리적 상태(logical statement)로 classification을 해석할 수 있음 → logical statement = rules
> root에서 leaf node까지 가는 길은 rule을 표현함
> 속성으로 구성된 각 rule은 AND로 연결된 길을 따라 test 함

# Probability Estimation (확률 추정)
- 가끔 분류보다 확률 추정을 원함
ex) 그는 채무 불이행을 하지 않음 → 그가 채무 불이행을 할 확률 = 40%, 반대의 경우 = 60%
> 더 정교한 decision-making을 할 때 사용 ex) 순위 매기기
> 같은 write-off에 classification 되어도 write-off의 확률이 51%여서 분류된 것과
90%여서 분류된 것은 느낌이 다름
- probability estimation tree
> class의 예측뿐만 아니라 각
leaf node는 class의 membership 확률의 추정치를 제공함

# Constructing Probability Estimate Tree
- classification tree를 만드는 것 대신 probability estimation tree를 쉽게 만들 수 있음
> 같은 tree induction idea를 사용함

- Frequency-based probability estimation (빈도 기반 확률 추정)
> class probability estimation을 계산하기 위해 각 leaf의
instance 개수를 사용
> leaf가 n개의 positve instance와 negative instance
m개를 가지면, 새로운 instance가 positive에 속할 확률은
아마 n/n+m일 것 임 → 빈도 기반 추정
# Overfitting of Probability Estimation Tree
- overfitting 문제
> instatance 수가 매우 적은 segment의 class membership 확률에 대해 지나치게 낙관적임
→ 오직 단일 instance만 가지는 leaf에서 100%의 확률이라고 할 수 있는가?
- Laplace correction
> 단순 빈도를 계산하는 것 대신 빈도 기반의 추정의 'smoothed' 버전을 사용함
→ frequency-based estimate = n/n+m
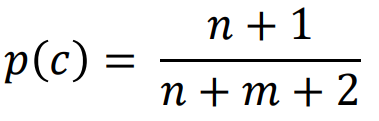
class c에 속하는 n, class c에 속하지 않는 m
분자의 +1과 분모의 +2는 점근선이 되게 하는 역할 → 점근선이 smoothed 된 버전을 의미
# Example of Laplace Correction
- leaf node의 확률
> p1: 2개의 positive와 negative는 없음
> p2: 20개의 positive와 negative는 없음
- 빈도 기반 추정: p1 = p2 = 1
- Laplace correction
> p1: 0.75 = 3/4 ((2+1)/(2+2))
> p2: 약 0.95 = 21/22 ((20+1)/(20+2))
> 같은 비율이더라도 instance의 개수가 증가할수록 확률이 증가
> p2를 p1보다 더 높게 추정함
# Effect of Laplace Smoothing
- instance의 수가 증가할수록, Laplace 방정식이 빈도 기반 추정에 수렴됨
> 다른 class 비율 (2/3, 4/5, 1/1)
> 변하지 않는 선은 Laplace방정식의 점근선임

* Line: 변하지 않는 추정
* Dashed Line: Laplace 방정식이 적용됨
# Churn Prediction Problem
- 가지고 있는 데이터를 기반으로 이탈할 고객을 추측함
- 가지고 있는 데이터
> 20,000명의 historycal data set
> 각 고객은 아래 속성에 의해 묘사됨

- 첫 번째: 이 속성들은 각각 얼마나 좋은가?
> 이를 알아보기 위해 각 속성에 대해 information gain을 측정할 수 있음 → measure the information gain

- 고객 이탈 data로부터 학습된 classification tree

- House: 전체 instance 집합에 대한 가장 높은 information gain 특징
- INCOME: HOUSE subgroup(house>600469)에 대한 가장 높은 information gain 특징
- class decision에 대한 문턱 확률 = 0.5
→ prob >= 0.5 이면 class는 CHURN, 아니라면 STAY
- 언제 tree 구축을 멈춰야 하는지? (→5장에서 자세히 배움)
> 20,000개의 예시가 있다면 20,000개의 leaf를 가질 때까지 나눠야 하는가? → YES
>> 하지만 model이 복잡해지기 전에 멈춰야 함
> 이 문제는 모델의 일반성과 overfitting과 밀접한 관련이 있음
- tree의 정확성을 어떻게 측정할 수 있는지? (→5장에서 자세히 배움)
> 원래 dataset에 적용했을 때 그 정확성이 73%를 달성했다고 가정해보자
> 이것은 믿을 수 있는 수치인가? → 다른 dataset을 사용했을 때도 73% 성취율을 보일 것인가?
> 이것이 좋은 모델임을 의미하는가? → 이것은 73% 정확성을 가지는 사용하는데 가치 있는 모델인가?
# Summary
- Predictive modeling
> One of the main tasks of data science
> Build a model and use the model to estimate the value of a target for a new unseen example
- Finding and selecting informative attributes
> A useful data mining procedure in and of itself → 유용한 data mining 절차 그 자체
> Find those attributes that give us information about another attribute
> One basic measure is information gain, which is based on a purity measure called entropy
- Tree induction
> A common modeling technique based on selecting informative attributes
> Recursively finds informative attributes for subsets of the data
> The resulting tree-structured model partitions the space of all possible instance
into a set of segments with different predicted values for the target
→결과 tree-structed model은 가능한 모든 instance의 공간을 target에 대해
서로 다른 예측 값을 가진 segment 집합으로 분할함
'Study > Data Science' 카테고리의 다른 글
| [DataScience] Ch6. Similarity, Neighbors, and Clusters (0) | 2021.08.24 |
|---|---|
| [DataScience] Ch5. Overfitting and Its Avoidance (0) | 2021.08.24 |
| [DataScience] Ch4. Fitting a Model to Data (0) | 2021.08.23 |
| [DataScience] Ch.2 Business Problems and Data Science Solutions (0) | 2021.08.23 |
| [DataScience] Ch1. Data-Analytic Thinking (0) | 2021.08.23 |
