Chapter 02. 구문법(Syntax)
프로그래밍 언어론 원리와 실제 - 창병모 교수님
2.1 구문 및 문법
Q. 가능한 문장 혹은 프로그램의 개수가 무한하지 않은가? 무한한 것들을 어떻게 유한하게 정의할 수 있는가?
A. 점화식 혹은 재귀식(recursive relation)을 이용하여 해결할 수 있음
1) 이진수의 구문법
- 이진수를 구성하는 방법
(1) 숫자(D)는 '0' 혹은 '1'이다.
(2) 이진수(N)를 구성하는 방법은 두 가지가 있는데
첫 번째 방법은 숫자(D) 하나로 구성하는 것이다.
두 번째 방법은 이진수(N) 다음에 숫자(D)를 하나 붙여서 구성하는 것이다.
- 논리 규칙 형태

- 문법 형태
N → D
N → ND
or
N → D | ND
- 이진수의 의미: 보통 이진수의 의미를 그 이진수가 의미하는 십진수 값으로 생각하는데 이것을 이진수의 시맨틱스라고 함
D → '0' V('0') = 0
D → '1' V('1') = 1
N → D V(D)
N → ND V(ND) = V(N) * 2 + V(D)
+) 십진수: 구문법과 의미론

2) 수식의 구문법
[수식 문법 1] 이 규칙에 따라 덧셈과 곱셈을 사용하는 수식들을 작성할 수 있음
E → E + E (1)
| E * E (2)
| ( E ) (3)
| N (4)
N → N D | D
D → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
- 수식의 의미

- 3 * 5 + 12의 의미인 값을 계산
V(3 * 5 + 12) = V(3 * 5) + V(12) = V(3) * V(5) + V(12) = 3 * 5 + 12 = 27
3) 프로그래밍 언어의 구문 구조
Q. 프로그래밍 언어의 구문 구조를 어떻게 표현할 수 있을까?
A. 재귀를 이용한 구문법으로 정의
- 프로그래밍 언어의 문장은 언어에 따라 여러 종류가 있는데 가장 기본적인 문장이 대입문(assignment statement), 조건문(conditional statement), 반복문(repeat statement) 등이 있음
(1) id = E // 식별자(id)에 수식(E)을 대입하는 대입문
(2) if E then S else S // 수식(E)의 값에 따라 실행할 문장을 결정하는 if문의 구조
(3) while ( E ) S // 수식(E)이 참일 동안 문장 S를 반복하는 while문의 구조
S: 임의의 문장 → 어떤 문장이라도 올 수 있음
- 재귀적 정의를 이용하여 프로그래밍 언어의 문장 S의 구문법을 정의해 봄
S → id = E
| if E then S else S
| while ( E ) S
| ...
이 문법은 문맥-자유 문법이라고 하며 문맥-자유 문법은 이러한 재귀적 구조를 자연스럽게 표현할 수 있음
4) 문맥-자유 문법(CFG: Context-free grammar)
- 구성
- 터미널 심볼의 집합 T
- 넌터미널 심볼의 집합 N
- 시작 심볼 S(넌터미널 심볼 중에 하나)
- 다음과 같은 형태의 생성(문법) 규칙들의 집합

- 넌터미널(nonterminal) 심볼: 넌터미널 심볼이 나타내는 스트링의 작성법이 문법 규칙에 의해 정의되어 있음 → 문법 규칙의 왼쪽에 위치할 수 있으며 일종의 구문적 변수 역할을 함
- 터미널(terminal) 심볼: 더 이상 작성법이 정의되어있지 않으며 문법 규칙에 오른쪽에만 나타날 수 있음
5) 생성 규칙
- 생성 규칙 또는 문법 규칙
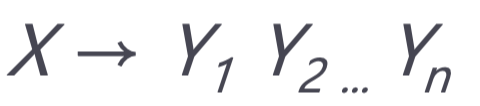
- X를 작성하는 방법을 정의하는 문법 규칙
- X는 Y1 Y2 .... Yn 형태로 작성할 수 있다는 것을 의미
- X를 작성하는 방법이 여러 가지가 있을 수 있으므로 X로 시작하는 규칙도 여러 개 있을 수 있음
6) 언어 S의 문장 요약 문법
Stmt S → id = E
| S; S
| if E then S
| if E then S else S
| while ( E ) S
| read id
| print E
Expr E → n | id | true | false
| E + E | E - E | E * E | E / E | ( E )
| E == E | E != E | E < E | E > E | !E
2.2 유도
1) 유도
Q. 어떤 문장 혹은 프로그램이 구문법에 맞는지는 어떻게 검사할 수 있을까?
A. 일반적으로 입력된 스트링이 맞는지 검사하려면 문법으로부터 유도(derivation)해보아야 함
- 어떤 스트링이 문법으로부터 유도 가능하면 문법에 맞는 스트링이고, 그렇지 않으면 문법에 맞지 않는 스트링임
- 유도: 생성 규칙을 적용하여 문법에 맞는 문장 혹은 스트링을 생성하는 과정
- 핵심 아이디어
- 시작 심볼 S부터 시작한다
- 넌터미널 심볼 X를 생성규칙을 적용하여 Y1 Y2 .... Yn으로 대치한다
- 이 과정을 넌터미널 심볼이 없을 때까지 반복한다
- 생성 규칙 X → Y1 Y2 ... Yn 적용
- X → Y1 Y2 .... Yn으로 대치
- X가 Y1 Y2 .... Yn을 생성
- 터미널 심볼
- 대치할 규칙이 없으므로 일단 생성되면 끝
- 터미널 심볼은 그 언어의 토큰
- 유도 예시
S → aS | b 즉, {a^nb | n≥ 0}
S => aS => aaS => aaaS => aaab
- 직접 유도(Direct derivation)
- 생성 규칙을 한 번 적용. 즉, 생성 규칙의 왼쪽 터미널 심볼을 오른쪽 심볼로 대치하는 것
- 생성 규칙 Xi → Y1 Y2 ... Yn이 존재하면
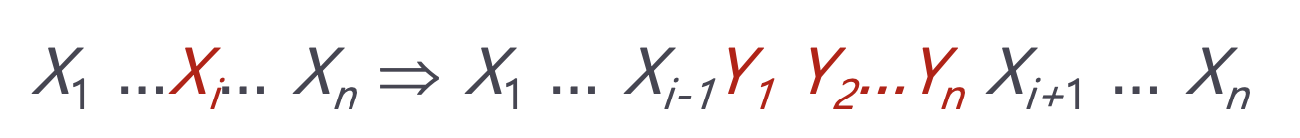
- 유도(Derivation) =>*
- 생성 규칙을 여러 번 적용. 즉, 직접 유도를 연속적으로 하는 것
- 0번 혹은 그 이상 번의 직접 유도가 가능하면 =>* 기호로 나타냄
- X1 ... Xn => .... => Y1 ... Ym이 가능하면

[수식 문법 2] 해당 수식 문법을 사용하여 스트링 3 + 4 * 5를 유도해보기
E → E + E
| E * E
| ( E )
| N
N → N D | D
D → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
E => E + E => N + E => D + E => 3 + E => 3 + E * E => 3 + N * E => 3 + D * E => 3 + 4 * E => 3 + 4 * N
=> 3 + 4 * D => 3 + 4 * 5
2) 좌측 유도와 우측 유도
- 유도는 각 직접 유도 단계에서 어떤 넌터미널이나 선택하여 생성 규칙을 적용할 수 있음. 하지만 일관되게 선택하는 것이 좋음
- 좌측 유도: 각 직접 유도 단계에서 가장 왼쪽 터미널을 선택하여 이를 대상으로 생성 규칙을 적용 → 지금까지 한 유도가 좌측 유도의 예시
- 우측 유도: 각 직접 유도 단계에서 가장 오른쪽 넌터미널을 선택하여 이를 대상으로 생성 규칙을 적용하면 됨
- 우측 유도 예시: 3 + 4 * 5
E => E * E => E * N => E * D => E * 5 => E + E * 5 => E + N * 5 => E + D * 5 => E + 4 * 5=> N + 4 * 5
=> D + 4 * 5 => 3 + 4 * 5
3) 문법 G의 언어
- 문법 G에 의해 정의되는 L(G)는 문법 G에 의해서 유도되는 모든 스트링의 집합
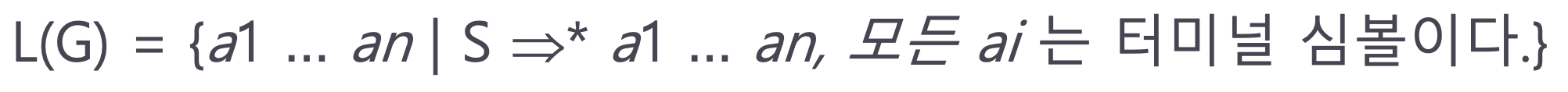
- 예: 문법 G
S → ( S )
S → a
1. 먼저 몇 개의 가능한 스트링을 유도(생성) 해 보면 다음과 같음
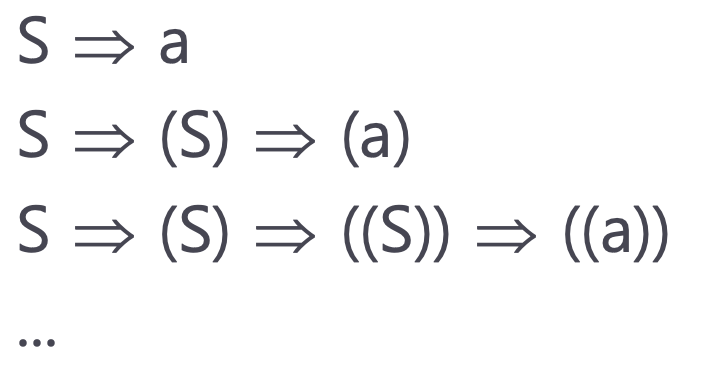
2. 이들을 집합 형태로 표현해 봄

4) 유도 트리
- 유도 트리(Derivation tree)
- 유도 과정 혹은 구문 구조를 보여주는 트리
- 유도 트리 = 파스 트리 = 구문 트리
- 유도는 시작 심볼로부터 시작하여 연속적으로 직접 유도를 함
S => ... =>
- 이러한 유도 과정은 다음과 같이 트리 형태로 그릴 수 있음
- S가 트리의 루트이다
- 규칙 X → Y1 Y2 ... Yn을 적용하여 직접 유도를 할 때마다 X노드는 Y1, ..., Yn를 자식 노드로 갖도록 트리를 구성한다
- 예: 3 + 4 * 5 를 유도하는 전체 과정을 트리 형태로 구성
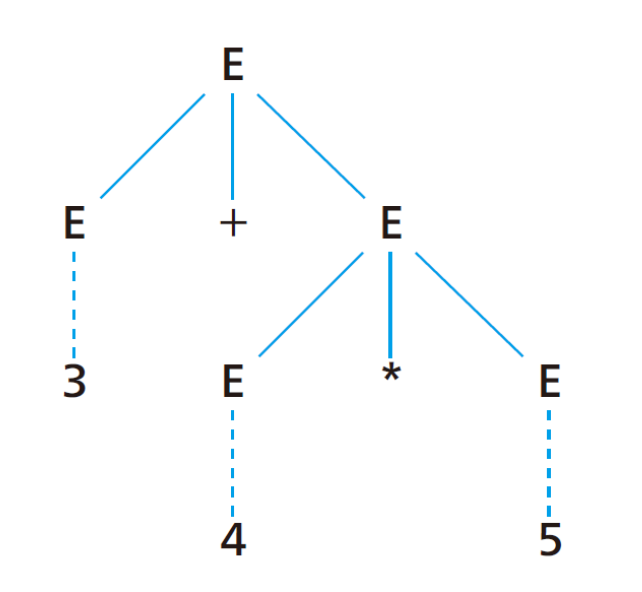
- 주의
- 좌측 유도와 우측 유도 모두 같은 파스 트리를 가짐
- 차이점은 파스 트리에 가지가 추가되는 순서
2.3 모호성
1) 모호성
- [수식 문법 2]를 사용한 스트링 3 + 4 * 5 스트링은 2개의 파스 트리를 가질 수 있음
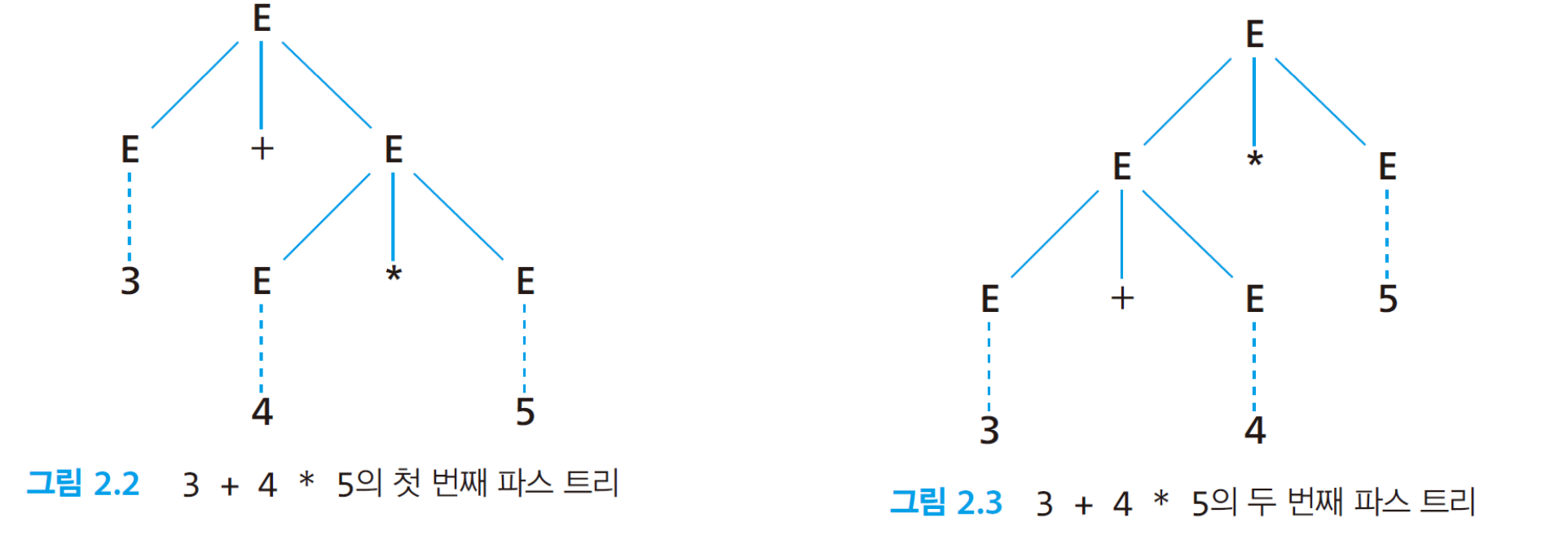
파스 트리의 구조에 따라 그 의미가 달라짐
그림 2.2의 의미는 23이 되고, 그림 2.3의 의미는 35가 되기 때문임
- 모호한 문법(ambiguous grammar): 어떤 스트링에 대해 두 개 이상의 좌측 유도(혹은 우측 유도)를 갖는 문법
- 모호한 문법은 어떤 스트링에 대한 구조를 두 개 이상으로 해석할 수 있기 때문에 좋지 않은 성질임
- 해결 방법
- 모호한 문법을 같은 언어를 정의하는 모호하지 않은 문법으로 재작성한다
- 언어의 구문법을 모호하지 않도록 일부 수정
2) 모호성 처리 방법 1
- 문법 재작성: 원래 언어와 같은 언어를 정의하면서 모호하지 않도록 문법 재작성
- 예시 : 수식 문법을 모호하지 않도록 재작성
- 우선순위를 적용하여 모호하지 않도록 재작성
- 수식은 여러 개의 항들을 더하는 구조
[수식 문법 3] 이 문법을 사용하여 3 + 4 *5에 대해서 단 하나의 좌측 유도만 가능해짐을 확인할 수 있음
E → E + T | T
T → T * F | F
F → M | ( E )
E => E + T => * N + T => 3 + T => 3 + T * F => 3 + F * F => 3 + N * F =>* 3 + 4 * N =>* 3 + 4 * 5
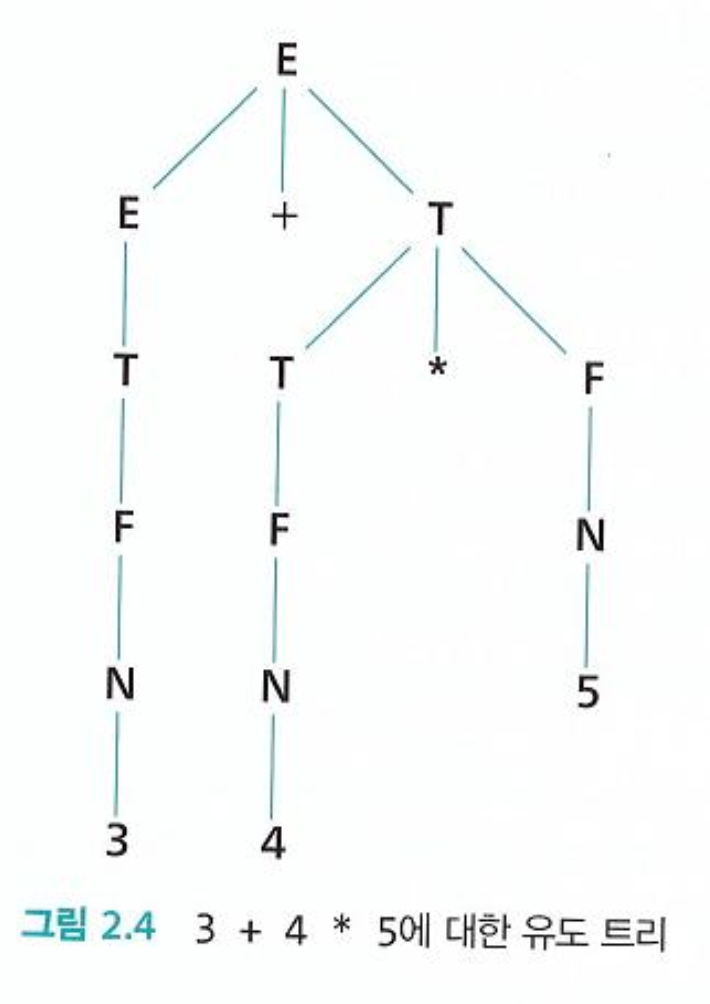
3) 모호성 처리 방법 2
- 언어 구문 일부 변경: 원래 언어와 약간 다른 언어를 정의하도록 언어의 구문을 일부 변경하여 모호하지 않은 문법 작성
- 예시: The Dangling Else
S → if E then S
| if E then S else S
if e1 then if e2 then s1 else s2라는 문장에 대해 두 개의 파스 트리가 존재하기 때문에 모호한 문법
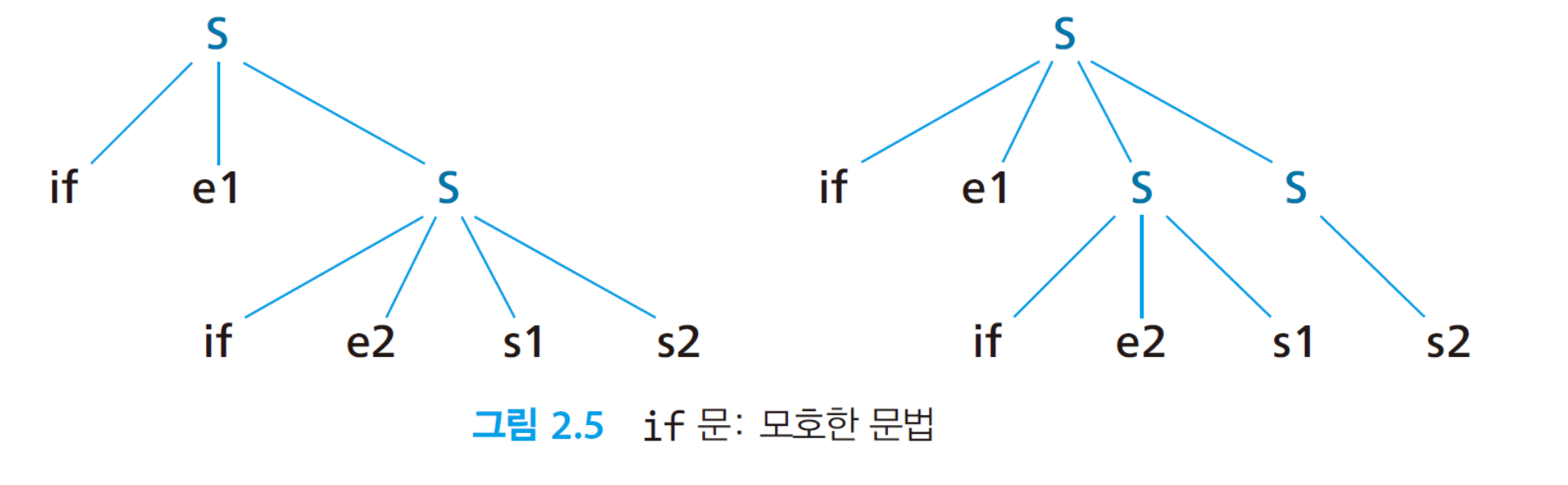
S → if E then S end
| if E then S else S
다음과 같이 if-then 문장은 반드시 end로 끝나게 변경하면 모호성이 사라짐
위에서 첫 번째 트리와 두 번째 트리를 다음과 같이 표현할 수 있음
1. if e1 then e2 then s1 else s2 end
2. if e1 then if e2 then s1 end else s2
2.4 BNF와 구문 다이어그램
1) BNF
- 넌터미널을 화살괄호<..> 형태로 작성하는데 이렇게 하면 긴 이름의 넌터미널 심볼도 보다 분명히 표시하여 작성할 수 있음
- BNF 형식으로 작성된 문법은 재귀적으로 정의되어 있기 때문에 초보자들에게는 어려울 수 있음 → EBNF의 제안 배경
[수식 문법 4]
<expr> → <expr> + <term> | <term>
<term> → <term> * <factor> | <factor>
<factor> → number | ( <expr> )
2) EBNF
- EBNF의 핵심 아이디어: 재귀적 정의를 반복적 정의 형태로 표현하는 것
- {...}: 괄호 안의 것이 여러 번(0번 이상) 반복된다는 것
- [...]: 0번 이상 1번 (optional)
[언어 S의 문법: EBNF]
<stmt> → id = <expr>;
| '{' {<stmt>} '}'
| if ( <expr> ) then <stmt> [else <stmt>]
| while ( <expr> ) <stmt>
| read id;
| print <expr> ;
<expr> → <bexp> {& <bexp> | '|' <bexp> } | !<expr> | true | false
<bexp> → <aexp> [<relop> <aexp>]
<relop> → == | != | < | > | <= | >=
<aexp> → <term> {+ <term> | - <term>}
<term> → <factor> {*<factor> | / <factor>}
<factor> → [-] ( number | ( <aexp> ) | id )
3) 구문 다이어그램
- 구문 다이어그램
- 각 생성 규칙을 다이어그램으로 표현
- 넌 터미널: 사각형
- 터미널: 원
- 순서: 화살표
[수식 문법 6]
<expr> → <term> {+<term> | -<term>}
<term> → <factor> { * <factor> | / <factor> }
<factor> → number | ( <expr> )
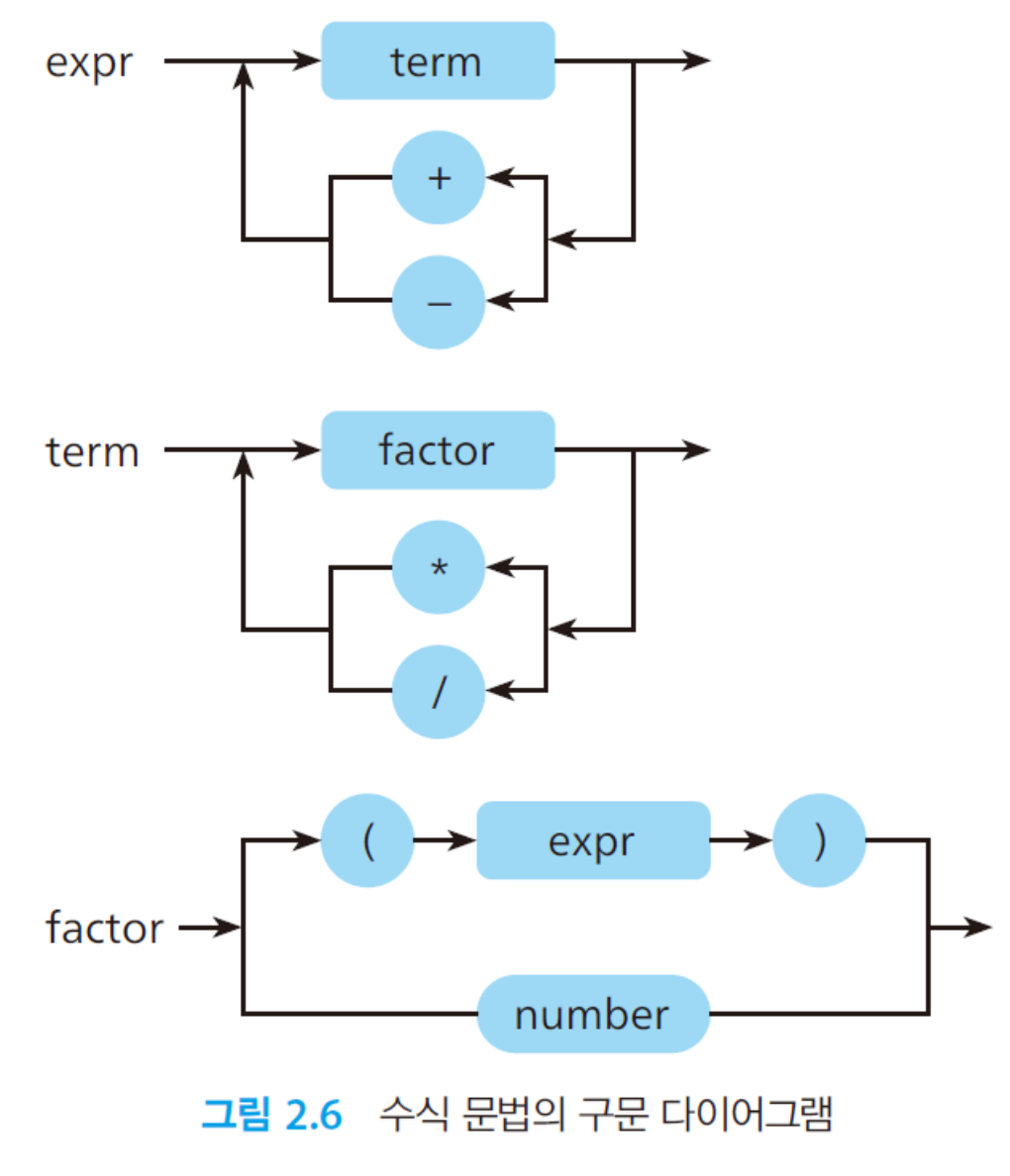
EBNF에서 중괄호로 나타낸 반복은 다이어그램에서 루프를 사용함
expr을 위한 다이어그램: 화살표를 따라가면서 루프를 돌아 term을 여러 번 반복할 수 있음
2.5 재귀 하강 파싱
1) 재귀 하강 파싱(recursive-descent parsing)
- 파싱: 입력 스트링을 유도하여 문법에 맞는지 검사
- 파서: 입력 스트링을 유도하여 문법에 맞는지 검사하는 프로그램
- 재귀 하강 파서의 기본 원리: 입력 스트링을 좌측 유도하도록 문법으로부터 직접 파서 프로그램을 만듦
2) 재귀 하강 파싱 구현
- 각 넌 터미널: 하나의 프로시저(함수, 메소드)를 구현
- 프로시저 내: 생성 규칙 우변을 적용하여 좌우선 유도하도록 작성
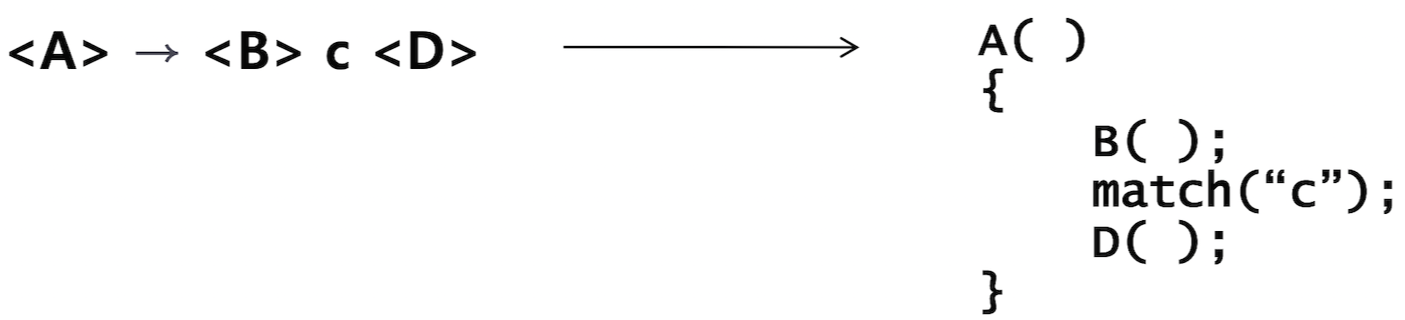
프로시저 호출: 생성 규칙을 적용하여 유도
match('문자'): 다음 입력(토큰)이 문자와 일치하는지 검사
'Study > Programming Language' 카테고리의 다른 글
| [PL] Chapter 04. 변수 및 유효범위 (2) | 2022.04.25 |
|---|---|
| [PL] Chapter 03. 언어 설계와 파서 구현 (0) | 2022.04.24 |
| [PL] Chapter 01. 서론 (0) | 2022.04.23 |
