# Polynomial A(x) = 3x^20 + 2x^5 + 4
- a sum of terms(항), ax^e (x: variable, a: coeffiecient(계수), e: exponent(지수))
# Operations of Polynomial ADT
- Zero(): 다항식을 0으로 만듦 ::= return 다항식, p(x) = 0
- IsZero(poly): 다항식이 0인지 검사 ::= if(poly) return FALSE
else return True
- Coef(poly, expon): 다항식에서 지수가 expon인 계수를 반환
- Lead_Exp(poly): 다항식에서 가장 큰 차수(지수의 값)를 반환
- Attach(poly, coef, expon): 계수가 coef이고 지수가 expon인 항을 추가
- Remove(poly, expon): 지수가 expon인 항을 제거
- SingleMult(poly, coef, expon): 계수가 coef이고 지수가 expon인 항 하나와 주어진 다항식 poly를 곱함
- Add(poly1, poly2): 주어진 두 다항식을 더함
- Mult(poly1, poly2): 주어진 두 다항식을 곱함
# Addition between polynomials 다항식의 덧셈
- d(polynomial) = a(polynomial) + b(polynomial)
- 다항식은 전체 다항식이 저장되는 것이 아닌 계수와 지수에 의해 표현됨
- 두 개의 다항식을 더할 때, 지수의 차수가 큰 것부터 순서대로 비교함 → 큰 차수부터 더해 나감
# Array of polynomial terms
#define MAX_TERMS 50
struct polynomial{
float coef; // 계수
int expon; // 지수
};
struct polynomial terms[MAX_TERMS];
/*구조체 polynomial을 형식으로하는 이름이 terms인 배열 → 크기는 MAX_TERMS*/
int avail = 0; // 배열의 인덱스를 나타냄
# Polynomial attach
- 계수가 coef이고 지수가 expon인 항을 추가
void attach(float coefficient,int exponent) {
if (avail >= MAX_TERMS) {
printf("Too many terms in the polynomial");
exit(1);
}
terms[avail].coef = coefficient;
terms[avail++].expon = exponent;
}
# Polynomial add
- D(x) = A(x) + B(x)
- A(x) = 2x^100 + 1
- B(x) = x^4 + 10x^3 + 3x^2 +1
- D(x) = 2x^100 + x^4 + 10x^3 + 3x^2 +2
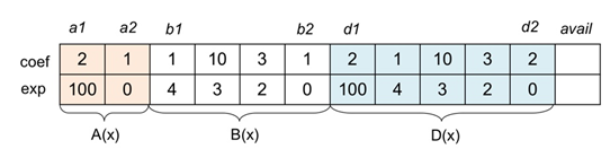
ex) padd(0,1,2,5,&d1,&d2)
> 0,1 : 첫 번째 polynomial의 시작과 끝 인덱스
> 2,5 : 첫 번째 polynomial의 시작과 끝 인덱스
> &d1,&d2 : 두 polynomial을 계산 한 결과는 시작과 끝이 있을 텐데
그것은 d1과 d2에 저장되기 때문에 d1, d2의 주소 값을 넘겨줌
void padd(int a1, int a2, int b1, int b2, int *d1, int *d2) {
float coefficient;
*d1 = avail; // polynomial의 시작과 끝을 저장할 포인터
while (a1 <= a2 && b1 <= b2) { // 비교할 항이 남아있는 동안
if (terms[a1].expon < terms[b1].expon) {
attach(terms[b1].coef, terms[b1].expon);
b1++;
}
if (terms[a1].expon > terms[b1].expon) {
attach(terms[a1].coef, terms[a1].expon);
a1++;
}
if (terms[a1].expon == terms[b1].expon) {
coefficient = terms[a1].coef + terms[b1].coef;
if (coefficient!=0) {
attach(coefficient, terms[a1].expon);
}
a1++, b1++;
}
}
for (; a1 <= a2; a1++) attach(terms[a1].coef, terms[a1].expon);
for (; b1 <= b2; b1++) attach(terms[b1].coef, terms[b1].expon);
*d2 = avail - 1;
}
'Study > Data Structure' 카테고리의 다른 글
| [DS] Euclidean algorithm(유클리드 호제법) 과 최대 공약수 (0) | 2021.08.26 |
|---|---|
| [DS] Recursion(재귀 호출) 과 함수 호출 과정 (0) | 2021.08.26 |
| [DS] 자료구조 개념 및 구현 Chapter 2 연습문제 (0) | 2021.08.25 |
| [DS] 볼링 게임 점수 계산 구현 (0) | 2021.08.25 |
| [DS] Array (배열) & Multi-Dimensional Array (다차원 배열) (0) | 2021.08.25 |
