# 배열
- 자료형이 동일한 원소(element)들의 유한 집합
- 연속적인 메모리상에서 표현되며 각 원소의 값은 고유의 인덱스(index)를 사용하여 접근
- 선형의 1차원 배열, 표 형식의 2차원 배열, 6면체 형태의 3차원 배열이 있음
- 2차원 이상의 배열은 다차원 배열(multi-dimensional array)라고 부름
- 배열의 인덱스는 0부터 1씩 증가하며, 2차원 배열은 (행, 열) 순서쌍으로 인덱스를 표현
- 배열은 선언된 이후에 배열의 크기(원소의 수)를 변경할 수 없기 때문에 필요한 원소의 수를 잘 예측해야 공간 부족 또는 메모리 낭비를 예방할 수 있음
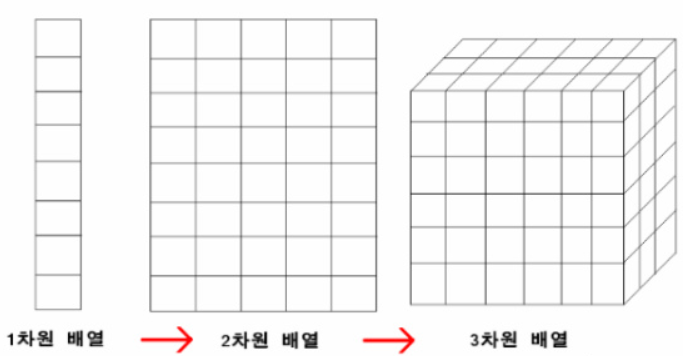
> 1차원 배열: 8개의 원소로 구성되는 배열
> 2차원 배열: 8행 5열로 구성되는 배열
> 3차원 배열: 6행 6열이며 폭의 길이가 3인 육면체 형태
# 배열의 선언
int A[5]; // 정수형 배열
int *ptr[5]; // 정수 포인터형 배열
int B[2][3]; // 2행 3열 정수형 배열
- 원소의 자료형, 배열 이름, 배열의 크기 순서로 선언
- 선언문에서 배열 이름 옆 대괄호 안의 숫자는 배열 원소의 수를 의미
- 배열 A의 원소 수가 n개 일 때
> 유효한 배열 인덱스의 범위: [0...n-1]
> 인덱스 0: 하한 경계(lower bound)
> 인덱스 n-1: 상한 경계(upper bound)
- 인덱스 범위를 벗어나는 원소를 참조할 경우 심각한 오류 발생할 수 있음
int list[5];- 1차원 배열은 연속적인 메모리 공간 상에서 표현되며, 한 개의 int형 원소에 4바이트를 할당
- 2차원 이상의 배열도 개념적으로는 다차원이지만 물리적으로는 1차원 메모리 상에 표현됨
- 배열의 첫 번째 원소인 list[0]의 주소를 시작 주소(base address: α)라고 함
- 각 원소의 주소는 4바이트씩 차이가 남 // α + i*sizeof(int)
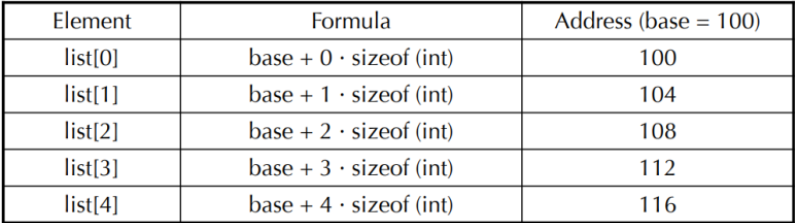
- 배열의 이름(list)는 시작 주소를 값으로 가지고 있는 포인터 상수(pointer constant) 임
int list[5]; // 포인터 상수
int * list2; // 포인터 변수
- 새로운 값을 자유롭게 저장할 수 있는 포인터 변수(item2)와 달리 배열 선언에 사용된 이름은 이후 다른 값(주소)을 가질 수 없음
- 배열 이름과 원소 간에는 다음의 관계가 성립
list == &list[0]
*list == list[0]
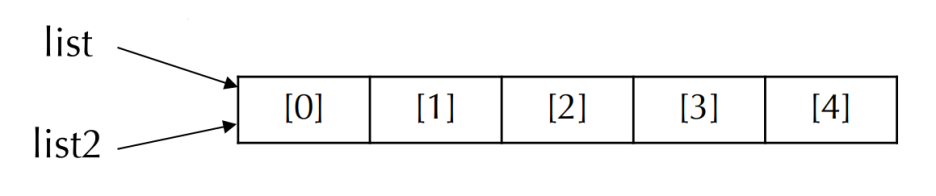
list2 = list;
list2[1] = 5;- list2에 list의 값을 할당하면 그림과 같이 두 포인터가 같은 메모리 공간을 공유하게 되며 list2에 인덱스를 사용해 배열의 원소에 접근할 수 있음
# 함수에 배열 전달
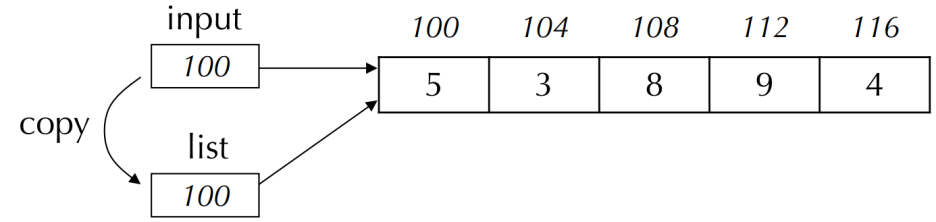
- 배열을 함수에 전달할 때 시작 주소를 가지고 있는 배열 이름을 전달하면 됨
> 배열 원소들을 일일이 복사할 필요 X
- 배열 포인터 관점: 값의 전달 (call by value)
- 배열 관점: 참조 전달 (call by reference)
sum(input, N); // 함수에 배열 전달
float sum(float list[], int n) // 배열을 받는 함수의 헤더- sum 함수에서 float list[]는 float *list와 동일한 표현
[코드]
#include <stdio.h>
#define ARRAY_SIZE 100
int arraySum(int num[], int n);
int main(void) {
int i, num[ARRAY_SIZE], result;
for(i=0;i<ARRAY_SIZE;i++)
num[i] = i;
result = arraySum(num, ARRAY_SIZE);
printf("The sum is: %d\n", result);
}
int arraySum(int num[], int n){
int i, temp=0;
for(i=0;i<n;i++)
temp+= num[i];
return temp;
}
[실행결과]

# 배열의 선언과 초기화
- 배열의 크기를 따로 지정하지 않고 다음과 같이 원소들로 초기화하면서 선언할 수 있음
int oneArray[] = {0, 1, 2, 3, 4}; // 배열 선언과 초기화- 배열 이름 oneArray에 정수를 더하면 배열의 첫 번째 원소에서부터 정수의 원소 개수만큼 떨어진 곳에 있는 원소의 주소를 의미
> oneArray의 값이 주소 100일 경우, oneArray+1은 104
> 따라서 다음과 같은 관계 성립 *(oneArray+1) == oneArray[1]
# 배열의 원소 출력
- 배열의 각 원소의 주소(address)와 저장된 값(value)을 출력하는 함수를 작성하시오.
(단, 원소의 개수(size)는 10으로 가정)
[코드]
#include <stdio.h>
void printArray(int *ptr, int size);
void main(){
int i, num[10];
for(i=0;i<10;i++)
num[i]=i;
printArray(num,10);
}
void printArray(int *ptr, int size){
int i;
for(i=0;i<size;i++){
printf("%8u %5d\t", ptr+i, *(ptr+i)); // 원소 i의 주소와 값
printf("%8u %5d\n",&ptr[i], ptr[i]);
}
}
[실행결과]
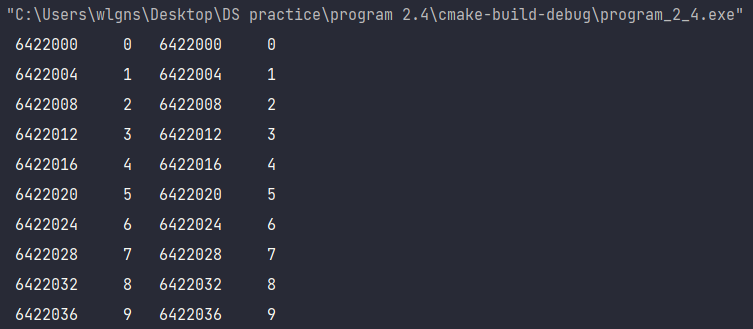
> 실행결과를 보면 주소 값이 4바이트씩 증가하는 것을 알 수 있는데
이는 정수 원소가 4바이트를 차지하기 때문임
# 다차원 배열
- 다차원 배열(multi-dimensional array): 2차원 이상의 배열
- 논리적으로는 m차원이지만, 물리적으로는 1차원 메모리 상에 표현됨
- m차원 배열 A
> int A[n0][n1]...[nm-1] (n0,n1, ...., nm-1은 각 차원의 원소의 수)
# 배열 표현 방법
- 다차원 배열의 표현
int A[n0][n1]...[n(m-1)]
- 배열 A에 저장되는 원소의 총 개수: n0 * n0 * .... * nm-1
ex) A[10][9][8]로 선언된 배열 원소의 총개수는 10*9*8로 720
- 다차원 배열 표현 방법: 행 우선 순서 / 열 우선 순서
(1) 행 우선 순서
- 오른쪽 인덱스(열)가 먼저 증가되고 상한 경계(upper bound)에 도달하면 왼쪽 옆자리(행)가 1 증가
- 인덱스 값이 오른쪽에서 왼쪽 방향으로 증가하면서 메모리에 저장됨
(2) 열 우선 순서
- 왼쪽 인덱스(행)가 먼저 증가되고 상한 경계(upper bound)에 도달하면 오른쪽 옆자리(열)가 1증가
- 인덱스 값이 왼쪽에서 오른쪽 방향으로 증가하면서 메모리에 저장됨
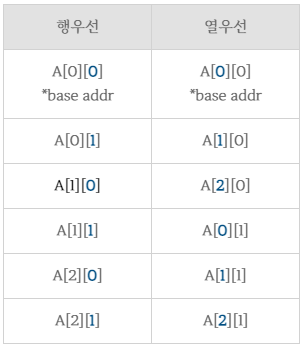
* base add: 기본 주소
- 배열에서의 원소의 위치: 시작 주소(base addr: α) + 오프셋(offset)
> 1차원 배열의 표현 (각 원소에 s 바이트가 할당된다고 가정): &A[i] = α + i * s (s=size of element)

# 2차원 배열의 표현
- A[n][m]인 배열이 있다 가정
(1) 행 우선 순위
- &A[i][j]: α + (i * m + j) * s
> 배열 원소 A[i][j] 앞에 i * m개의 원소가 존재 → 행 i(0 ~ i-1)개에 각각 m개의 원소가 있음
> i번 행에는 0 ~ j-1 즉, j개의 원소가 존재

(2) 열 우선 순위
- &A[i][j]: α + (i + j * n) * s
> 배열 원소 A[i][j] 앞에 j*m개의 원소가 존재 → 열 j(0 ~ j-1)개에 각각 m개의 원소가 있음
> j번째 열에는 0 ~ i-1 즉, i개의 원소가 존재

# 3차원 배열의 표현
- A[u0][u1][u2]인 배열이 있다 가정
- 평면을 구성하는 차원을 달리하면 주소 계산법에 차이가 있음
> 어느 평면을 기준으로 하는지에 따라서도 계산법에 차이가 있음

(1) 행 우선 순위 (u1 * u2 평면을 기준)
- &A[i][j][k]: α + (i * u1 * u2 + j * u2 + k) * s
> 앞에 존재하는 plane(u1 * u2)이 i개 존재
> 그다음부터는 2차원 배열 행 우선 순위와 동일함
(2) 열 우선 순위 (u1 * u2 평면을 기준)
- &A[i][j][k]: α + (i * u1 * u2 + j + u1 * k) * s
> 앞에 존재하는 plane(u1 * u2)이 i개 존재
> 그다음부터는 2차원 배열 열 우선순위와 동일함
'Study > Data Structure' 카테고리의 다른 글
| [DS] 자료구조 개념 및 구현 Chapter 2 연습문제 (0) | 2021.08.25 |
|---|---|
| [DS] 볼링 게임 점수 계산 구현 (0) | 2021.08.25 |
| [DS] Pointer (포인터) (0) | 2021.08.25 |
| [DS] 구조체 (0) | 2021.08.25 |
| [DS] 자료구조 개념 및 구현 Chapter 1 연습문제 (0) | 2021.08.25 |
