# 하노이 타워 (1)
- 세 개의 기둥과 크기가 다양한 원판들이 존재
> 초기 상태: 한 기둥에 모든 원판이 꽂혀 있음
- 목표: 한 기둥에 꽂힌 원판들을 그 순서 그대로 다른 기둥에 옮기는 것
- 조건
① 한 번에 하나의 원판만 옮길 수 있다
② 큰 원판이 작은 원판 위에 놓일 수 없다

- 알고리즘
더보기
세 개의 기둥 A, B, C가 있고 기둥 A에서 B로 n개의 원판을 옮긴다고 가정
1. 기둥 A에서 n-1개의 원판을 A, B가 아닌 기둥 C로 옮긴다
2. 기둥 A에 남은 1개의 원판을 B로 옮긴다
3. 기둥 C에 있는 n-1개를 기둥 B로 옮긴다
> 2번 과정: 1개의 원판이 이동하면 됨
> 1, 3번 과정: 원판의 수가 1개 줄어든 또 다른 하노이 타워 문제 → 재귀적인 방법으로 해결 가능
> 원판이 n개일 때 이동 횟수: 2n - 1
[코드]
#include <stdio.h>
int count =0;
void htower(int n, int a, int b);
int main() {
int n;
// count = 0; // 하노이 타워 문제를 여러 번 풀 때는 초기화 필요
printf("Enter disc number: ");
scanf("%d", &n); // 원판의 개수를 입력 받음
htower(n, 1, 2); // n개의 원판을 기둥 1번에서 2번으로 이동
printf("# move for %d discs : %d\n", n, count);
}
void htower(int n, int a, int b){
int c;
count ++;
if(n==1)
printf("Disc %d, moved from Pole (%d) to (%d)\n",n,a,b);
else{ // 원판의 개수가 2개 이상일 때
c = 6 -a-b; // 비어있는 기둥 c를 구하는 공식
htower(n-1,a,c); /* n-1개의 원판을 기둥 a에서 c로 이동
--> 기둥 a에서 남은 1개의 원판을 b로 이동*/
printf("Disc %d, moved from Pole (%d) to (%d)\n",n,a,b);
htower(n-1,a,b); // n-1개의 원판을 기둥 c에서 b로 이동
}
}
> 원판의 수가 1개씩 감소되면서 htower함수가 재귀호출되다가
원판의 수가 1개가 되면 더 이상 재귀호출이 발생하지 않음
[실행결과]

# 하노이 타워 (2)
- 알고리즘
더보기
세 개의 기둥 A, B, C가 있고 기둥 A에서 C로 n개의 원판을 옮긴다고 가정
1. 기둥 A에서 n-1개의 원판을 B로 옮긴다
2. 기둥 A에 남은 1개의 원판을 C로 옮긴다
3. 기둥 B에 있는 n-1개를 기둥 C로 옮긴다
> 1, 3번 과정 → 재귀적인 방법으로 해결 가능
> 원판이 n개일 때 이동 횟수: 2n - 1
[코드]
#include <stdio.h>
void hanoi_tower(int n, char from, char tmp, char to);
int main() {
int n;
printf("구하려는 원반의 개수를 입력하세요 :");
scanf("%d", &n);
printf("원반이 %d개 있을 때 하노이 탑의 결과\n\n",n);
hanoi_tower(n,'A','B','C');
}
void hanoi_tower(int n, char from, char tmp, char to){
if(n==1)
printf("원반 1을 %c에서 %c로 옮긴다. \n",from,to);
else{
hanoi_tower(n-1,from,to,tmp); // from: A, to: C, tmp: B
printf("원반 %d을 %c에서 %c으로 옮긴다. \n",n,from,to);
hanoi_tower(n-1,tmp,from,to); // from: tmp(B), to: from(A), tmp: to(C)
}
}
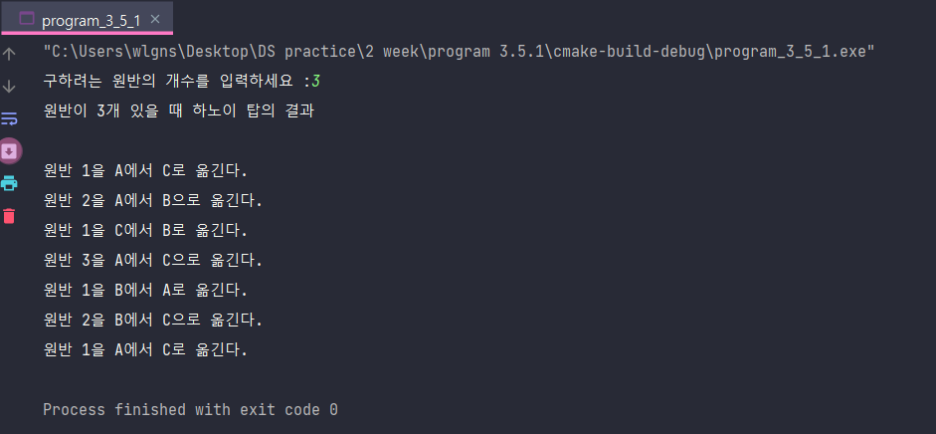
[실행결과]
'Study > Data Structure' 카테고리의 다른 글
| [DS] 자료구조 개념 및 구현 Chapter 3 연습문제 (0) | 2021.08.26 |
|---|---|
| [DS] Permutation (순열) (0) | 2021.08.26 |
| [DS] Euclidean algorithm(유클리드 호제법) 과 최대 공약수 (0) | 2021.08.26 |
| [DS] Recursion(재귀 호출) 과 함수 호출 과정 (0) | 2021.08.26 |
| [DS] Polynomial (다항식) (0) | 2021.08.25 |
