자료구조 개념 및 구현
Chapter 4. 알고리즘 분석 - 연습문제
Q1. 점근적 표기법(asymptotic notation)을 사용하는 이유를 적으시오.
- 알고리즘의 성능을 비교하기 위해 사용함. 입력의 수가 매우 커질 때, 알고리즘의 복잡도가 증가하는 패턴을 살펴봄
Q2. 시간 복잡도와 공간 복잡도는 각각 무엇을 의미하는가?
- 시간 복잡도: 프로그램이 수행을 완료하는데 걸리는 시간
- 공간 복잡도: 알고리즘 실행에 필요한 메모리
Q3. 시간 복잡도에 대한 점근적 표기법의 세 가지 종류를 각각 설명하시오
- 상한선(Big-Oh) 표기법: 시간 복잡도 함수 f(n) = Ο(g(n))이라고 표기할 수 있다면, 이 알고리즘의 수행 시간은 상한선 c·g(n)을 넘지 않는다는 의미
- 하한선(Big-Omega) 표기법: n0 이상 모든 n에 대해서 f(n)의 수행 시간은 하한선인 c·g(n)보다 항상 많이 걸림
- 상한-하한선(Big-Theta) 표기법: n0 이상 큰 모든 n에 대해서 f(n)의 수행 시간은 하한선(c1·g(n))과 상한선(c2·g(n)) 사이에 존재
Q4. 다음 관계식의 의미를 그래프를 그려서 설명하시오
f(n) = O(g(n))

Q5. 다음 관계식의 의미를 그래프를 그려서 설명하시오
f(n) = Θ(g(n))

Q6. 다음 관계식의 의미를 그래프를 그려서 설명하시오
f(n) = Ω(g(n))

Q7. 다음은 알고리즘의 시간 복잡도 함수이다. n이 충분히 클 경우 처리 속도가 가장 빠른 것부터 느린 순서로 나열하시오
{ n!, n log2 n, log2 n, 1, 2^n, n^100, n^3, n }
- 1, log2 n, n, n log2 n, n^2, n^100, 2^n, n!
Q8. 다음 함수의 시간 복잡도와 공간 복잡도를 각각 구하시오
int factorial(int n) // 4byte
{
if(n > 0) // n + 1 반복
return n * factorial(n - 1); // 4n byte, n
return 1; // 1
}
- 시간 복잡도: 2n+2
- 공간 복잡도: 8n
Q9. 다음 함수의 실행 시 필요로 하는 가변 메모리 공간 크기를 분석하시오
float recur_sum(float num[], int n) // 4 4
{
if(n)
return recur_sum(num, n - 1) + num[n - 1]; // 4n
else
return 0;
- 12n bytes (n, 배개변수 2개, return address)
Q10. 다음 함수의 시간 복잡도를 구하시오
#define SIZE 100
void add(int *X, int *Y)
{
int i, j;
int Z[SIZE][SIZE][SIZE];
for (i = 1; i < width; i++) // width
for(j = 1; j < height; j++) // (width-1) * height
for(k = 1; k < depth; k++) // depth * (height - 1) * (width - 1)
Z[i][j][k] = X[i][j][k] + Y[i][j][k]; // (width - 1) * (height - 1) * (depth -1)
- width + (width-1)*height + depth*(height-1) *(width-1) + (width - 1) * (height - 1) * (depth -1)
Q11. 다음 시간 복잡도 함수의 점근적 표기법을 그래프로 설명하시오
(1) 8n2 + 3n + 2 ≠ O(n)
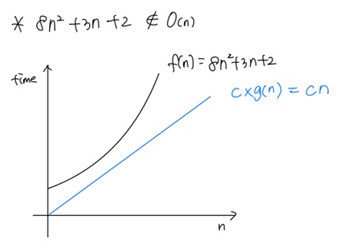
> 상수 c가 아무리 커져도 어느 지점 이상에서 주어진 함수 f(n)이 c·g(n) 이상이 되므로 성립하지 않음
(2) log2n + n + 3 = O(n)
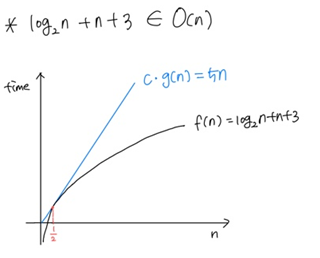
> c = 5, n0 = ½ 일 때 n > ½ 범위 내에서 주어진 함수의 수행 시간은 c·g(n)를 넘지 않으므로 성립함
(3) 10n2 + 4n +2 ≠ O(n)
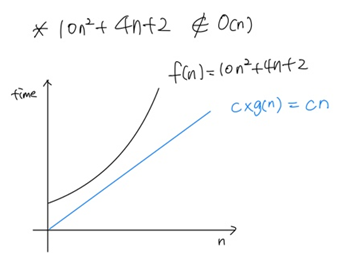
> 상수 c가 아무리 커져도 어느 지점 이상에서 주어진 함수 f(n)이 c·g(n) 이상이 되므로 성립하지 않음
(4) 3n + 2 = Θ(n)
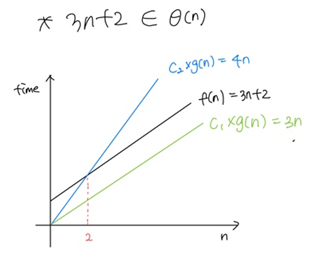
> c1 = 3, c2 = 4, n0 = 2 일 때 n > 2 범위 내에서 주어진 함수 f(n)이 c1·g(n) ≤ f(n) ≤ c2·g(n)의 관계를 만족하므로 성립함
Q12. 다음 시간 복잡도 함수를 Big Oh 표기법으로 표현하고 그 이유를 쓰시오
(1) log2n + n +3
- Ο(log2n)
> g(n) = log2n, c=4, n0 = 9 라 할 때, n>9 인 범위에서 주어진 함수의 수행시간은 c·g(n)를 넘지 않음
(2) nlog2n +n
- Ο(nlog2n)
> g(n) = nlog2n, c=2, n0 = 2 라 할 때, n>2 인 범위에서 주어진 함수의 수행시간은 c·g(n)를 넘지 않음
Q13. 시간 복잡도 Big Oh 표기법으로 적고 그것이 성립하는 이유를 밝히시오
(1) 10n2 + 4n + 2
- Ο(n2)
> g(n) = n2 , c=16, n0 = 1라 할 때, n>1 인 범위에서 주어진 함수의 수행시간은 c·g(n)를 넘지 않음
(2) 6·2n + n2
- Ο(2n)
> g(n) = 2n , c=7, n0 = 2라 할 때, n>2 인 범위에서 주어진 함수의 수행시간은 c·g(n)를 넘지 않음
Q14. 다음 관계식의 의미를 그래프를 그려 설명하시오
(1) 3n + 2 ≠ Ο(1)

> n > ⅓ 인 범위에 대하여 주어진 함수 f(n)이 c*1 이상이므로 성립하지 않음
(2) 3n + 2 = Θ(n)

> n > 2 인 범위에 대하여 주어진 함수 f(n)이 c1·g(n) ≤ f(n) ≤ c2·g(n) 관계를 만족하므로 성립
Q15. 다음 시간 복잡도를 Big Oh 형식으로 표기하고, 수행 속도가 빠른 것 부터 1, 2, 3, ... 으로 순위를 표시하시오 (동일 순위는 같은 번호로 표시할 것)
| 시간 복잡도 | Big Oh 표기법 | 실행 속도 순위 |
| 10n^3+4n^2+2 | O(n^3) | 3 |
| 6·2^n | O(2^n) | 4 |
| 1000nlog2 n+6 | O(nlog2 n) | 2 |
| 2log2 n+300 | O(log2 n) | 1 |
| c1n^3+c2n | O(n^3) | 3 |
| n!+n | O(n!) | 5 |
'Study > Data Structure' 카테고리의 다른 글
| [DS] Stack (스택) (0) | 2021.08.31 |
|---|---|
| [DS] Sparse Matrix (희소 행렬) (0) | 2021.08.26 |
| [DS] 알고리즘 분석 (0) | 2021.08.26 |
| [DS] 자료구조 개념 및 구현 Chapter 3 연습문제 (0) | 2021.08.26 |
| [DS] Permutation (순열) (0) | 2021.08.26 |
