자료구조 개념 및 구현
Chapter 5. 선형 자료구조 - 연습문제
Q1. 아래와 같이 선언된 배열 A가 메모리 상에 행 우선과 열 우선 순서로 각각 저장된다고 가정할 때 배열 원소 A[2][3][4]의 주소를 계산하시오
(단, &A[0][0][0] = 1000이고, sizeof(int) = 4 이다)
int A[9][7][8] ;(1) 행 우선 순서(row-major order)로 저장 시
- 1560 / 1000 + (2 * 7 * 8 + 3 * 8 + 4) * 4
(2) 열 우선 순서(column-mafor order)로 저장 시
- 1572 / 1000 + (2 * 7 * 8 + 3 + 4 * 7) * 4
Q2. 7x7 희소 행렬에서 0이 아닌 원소만을 3-순서쌍(row, column, value)으로 된 구조체 배열에 저장하려고한다. 이 방법이 2차원 배열에 행렬을 저장할 때보다 효율적이기 위해서는 0이 아닌 원소의 수가 최대 몇개 미만이어야 하는가? (단, 배열의 0번 원소는 배열의 정보 저장 용도로 사용한다고 가정한다)
- 16개
Q3. 배열 b에는 어떤 행렬의 0이 아닌 원소들만 순서쌍(row, col, value) 형식으로 저장되어 있다. 이 배열로부터 원래의 행렬 형식으로 원소를 출력하는 프로그램을 완성하시오. (배열 b의 0번 원소에는 원래 행렬의 row 수, col의 수, 0이 아닌 원소의 수가 저장되어 있다 가정한다)
[코드]
#include <stdio.h>
#define MAX_TERMS 101
struct term{
int row;
int col;
int value;
};
struct term b[MAX_TERMS];
int main() {
b[0].row=4;b[0].col=4;b[0].value=3;
b[1].row=0;b[1].col=0;b[1].value=1;
b[2].row=1;b[2].col=1;b[2].value=1;
b[3].row=2;b[3].col=2;b[3].value=1;
int i, j, k=1;
for(i=0;i<b[0].row;i++){
for(j=0;j<b[0].col;j++){
if(b[k].row==i&&b[k].col==j) {
printf("%3d", b[k].value);
k++;
}
else printf(" 0");
}
printf("\n");
}
}
[실행결과]

Q4. 시스템 스택과 활성 레코드(스택 프레임)의 목적과 작동 원리를 설명하시오
- 목적: 함수 호출을 관리하기 위해
- 작동 원리: 구조체 형태로 함수의 정보를 스택에 저장한 후 필요할 때 꺼내어 사용함
Q5. 다음 프로그램에 대한 질문에 답하시오
#include <stdio.h>
int F(int i){
if(i==0) return 1;
else return i*F(i-1);
}
void A(int *i){
*i = F(*i);
}
void main(){
int i=4;
A(&i);
printf("%d", i++);
}
(1) 다음 프로그램의 실행 결과를 쓰시오
- 24
(2) 위 프로그램이 실행되어 완료될 때까지 시스템 스택 상의 스택 프레임 변화 과정을 그림으로 설명하시오 (각 함수의 스택 프레임은 F(1), A(), main()의 형식으로 표시하시오)

Q7. 다음 프로그램이 실행되어 완료될 때까지 시스템 스택 상에서 활성 레코드의 변화 과정을 그림으로 설명하시오 (단, 각 함수의 활성 레코드는 main(), rsum(3), ...의 형식으로 표시하시오)
#include <stdio.h>
int rsum(int num[], int n);
void main(){
int num[]={2,3,4,5,6};
rsum(num,3);
}
int rsum(int num[], int n){
if(n) return rsum(num, n-1) + num[n-1];
else return 0;
}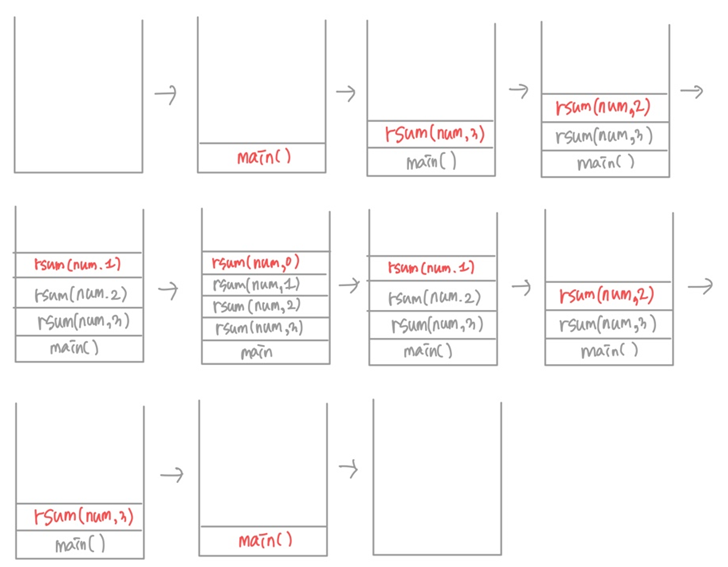
- rsum(n, 3)의 return 값: 9
Q8. 다음 각 수식을 지정된 표기법으로 변환하시오
(1) a b / c - d e * + a c * - (postfix → infix)
→ a / b - c + d * e - a * c
(2) 5 * 7 + (4 - 3) / 6 % 9 (infix → prefix)
→ + * 5 7 % / - 4 3 6 9
(3) a b c - d + / e a - * c * (postfix → infix)
→ a / (b - c + d) * (e - a) * c
(4) a b / c - d e * + a c * - (postfix → prefix)
→ - + - / a b c * d e * a c
(5) (a + b) * c + d / e + (f - g / h) * i (infix → postfix)
→ a b + c * d e / + f g h / - i * +
(6) a * ( b + c * d) / d - a * c (infix → prefix)
→ - / * a + b * c d d * a c
(7) - + - / a b c * d e * a c (prefix →postfix)
→ a b / c - d e * + a c * -
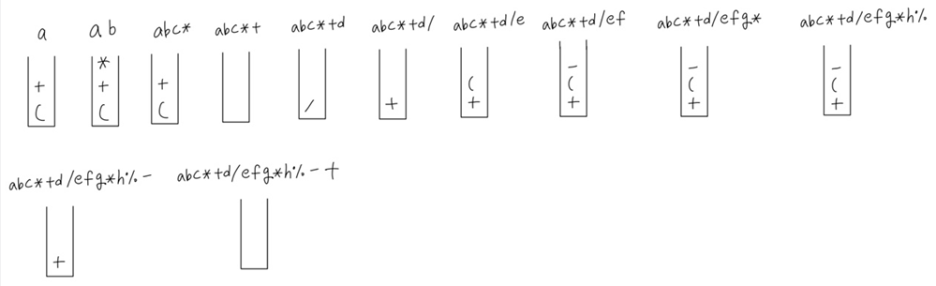
Q9. 다음 각 중위 수식을 후위 수식으로 스택을 이용하여 변환하는 과정을 보이시오
(1) 4 + (6 * 5 -9) / (3 * 2)

(2) (a + b * c) / d + (e - f * g % h)
Q10. 다음 수식에 대해서 질문에 답하시오
6 / (9 % 4 *2) - (5 + 7) * 3
(1) 주어진 수식을 전위 수식(prefix)으로 변환하시오
→ - / 6 * % 9 4 2 * 5 7 3
(2) 주어진 수식을 스택을 이용하여 후위 수식(postfix)으로 변환하는 과정을 보이시오

(3) (2)번 문제에서 생성된 후위 수식을 스택을 이용하여 계산하는 과정을 보이시오

Q11. 다음 수식을 전위 수식(prefix)로 변환하시오
5 + 9 / (7 - * 4) % 2
→ + 5 % / 9 - 7 * 3 4 2
Q12. 다음 후위 수식(postfix)을 중위 수식(infix)으로 변환하시오 (필요시 괄호를 사용할 것)
3 7 9 4 5 / - * 2 % +
→ 3 + 7 * (9 - 4 / 5) % 2
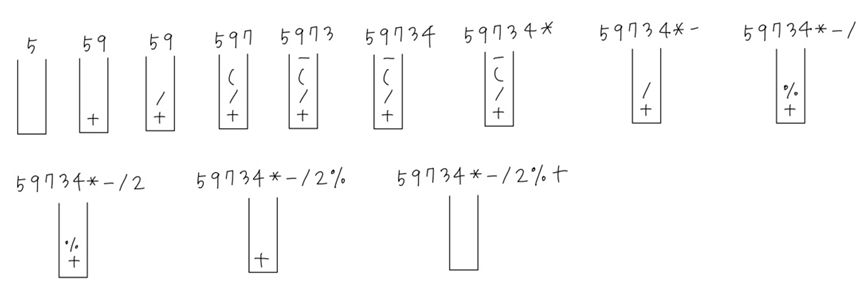
Q13. 다음 수식을 스택을 사용하여 후위 수식(postfix)으로 변환하고자 한다. 스택 내용의 변화 과정과 출력 결과를 보이시오
5 + 9 / (7 - 3 * 4) % 2
Q14. 다음 각 자료구조에 필요한 경계 조건(full/empty)을 주어진 변수/포인터를 이용하여 작성하시오 (단, 큐의 크기 = 스택 크기 = N이고, front, rear, top 변수는 모두 정수이다)
| 자료구조 | 포인터/변수 | full 조건 | empty 조건 |
| 순환 큐 | front/ rear | (rear+1)%N == front | f == r |
| 선형 큐 | front/ rear | rear == N-1 | f == r |
| 스택 | top | top + 1 == N | top == -1 |
Q15. 순환 큐(circular queue)가 필요한 이유를 일반 큐(ordinary queue)와 비교하여 쓰고, 일반 큐와 순환 큐의 경계 조건 및 최대 저장 가능 원소 수를 각각 쓰시오 (큐의 크기는 N이다)
- 일반 큐
> 빈 공간이 있더라도 full stack 상태로 인식 가능
> full 조건: rear = N - 1
> empty 조건: f == r
> 최대 저장 가능 원소 수: N
- 순환 큐의 경계 조건
> 공간 활용 가능
> full 조건: front == (rear+1)%N
> empty 조건: f==r
> 최대 저장 가능 원소 수: N-1
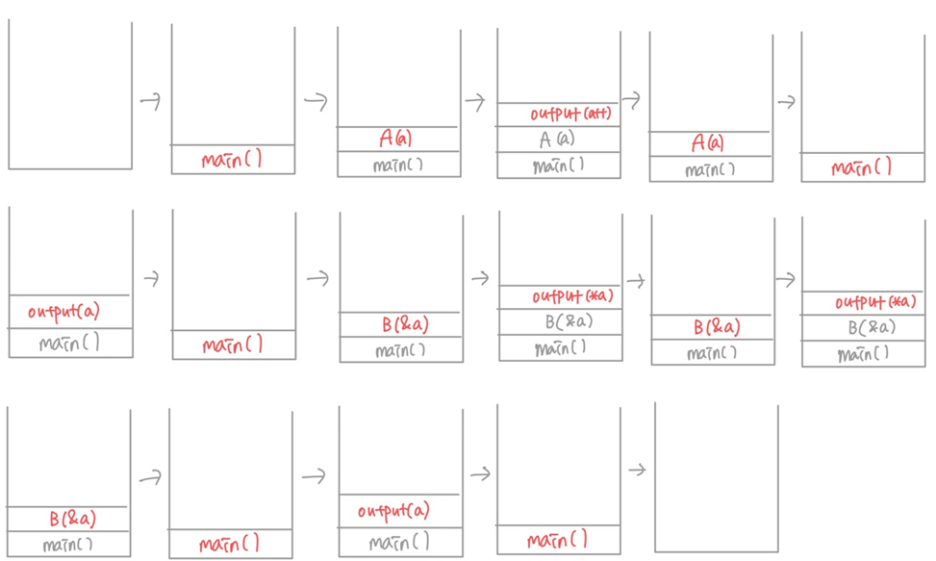
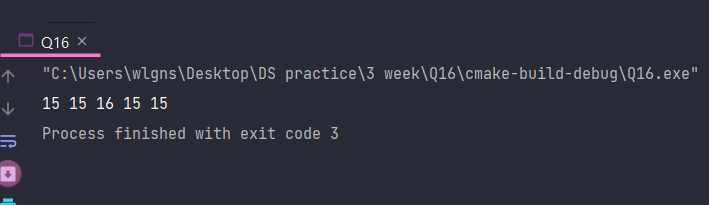
Q16. 다음 프로그램의 실행 결과를 쓰고, 시스템 스택에서 각 함수의 스택 프레임(활성 레코드)이 변환되는 내용을 쓰시오 (스택 프레임은 함수의 이름만 쓸 것)
#include <stdio.h>
void A(int a);
void B(int *a);
void output(int i);
void main(){
int a=15;
A(a);
output(a);
B(&a);
output(a);
}
void A(int a){
output(a++);
}
void B(int *a){
int *b = a;
++(*b);
output(*a);
(*a)--;
output(*a);
}
void output(int i){
printf("%d ", i);
}
[실행결과]
Q17. [실습] 후위 수식(postfix) 계산
다음과 같이 다중 숫자(multiple digit)로 구성된 후위 수식(postfix)의 값을 평가하는 프로그램을 작성하려고 한다. 다음 세부 기능을 구현하시오
2 14 * 23 +
| 세부 기능 | ||
| 1. gets()를 사용하여 postfix 수식을 입력받는다 2. 수식 평가 스택을 위한 push와 pop 함수를 구현한다 3. 다중 숫자를 변환하여 스택에 저장하는 코드를 작성한다 4. 수식 문자열에서 토큰을 입력받는 코드를 작성한다 5. 실행 결과와 같이 여러 개의 예를 사용하여 프로그램을 테스트한다. (토큰은 공백으로 구분한다) |
[실행결과 예시]

[코드]
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_STACK_SIZE 100
int evaluate();
void push(int item);
int pop();
char expr[30];
int top=-1;
int stack[MAX_STACK_SIZE];
int sym;
int sym_type;
void main(){
char expr2[30];
printf("Input a postfix expression :");
fflush(stdin);
gets(expr2);
strcpy(expr, expr2);
printf("%s\n", expr);
printf("evaluate of %s = %d",expr, evaluate());
}
void push(int item){
if(top>=MAX_STACK_SIZE-1){
printf("stack full");
return ;
}
stack[++top]=item;
}
int pop(){
if(top<0){
printf("stack empty");
return -999;
}
return stack[top--];
}
int evaluate(){
int num = 0, count = 0, value=0;
int length = strlen(expr); //expr 배열에 저장된 문자열의 길이
int op1, op2; // 연산자로 계산할 두 개의 숫자를 나타내는 변수 op1, op2
for (int i = 0; i < length;i++) {
sym = expr[i];//expr에서 i번째 인덱스에 해당하는 글자를 가져옴
if (sym >= '0' && sym <= '9') {// sym이 숫자이면
while (expr[i + count] != ' ') {// 띄어쓰기로 연산자와 피연산자를 구분하므로 띄어쓰기가 나타나기 전까지가 피연산자를 나타냄
count++;//count를 증가
}
value = atoi(&expr[i]);
/* 인덱스 i부터 시작함 atoi함수를 사용하였으므로 띄어쓰기를 만나면 더 이상 정수로 변환되지 않음 따라서 두 자릿수 이상의 수를 인식할 수 있음 */
i += count;// 읽어들인 수의 자리수만큼은 더 이상 검사할 필요가 없으므로 i에 count를 더해 i의 값을 변경
count = 0; // count를 다시 0으로 초기화함
push(value); // atoi함수로 변환 한 수를 stack에 push함
}
else if(sym!=' ') { // if의 조건이 아니며 expr에서 읽은 값이 ' ' 즉 띄어쓰기가 아닐 때 -> 연산자라는 의미임
op2 = pop();// op2()에 stack에서 값을 하나 꺼내 저장
op1 = pop();// op1()에 stack에서 다음 값을 하나 꺼내 저장
switch (sym) {// sym이 case에 맞는다면 각 명령문에 맞게 계산을 진행
case '+': push(op1 + op2); break;
case '-': push(op1 - op2); break;
case '*': push(op1*op2); break;
case '/': push(op1 / op2); break;
case '%': push(op1%op2); break;
}
}
}
return pop();// 계산이 끝나면 마지막에 stack에 남은 값이 우리가 계산한 결과값이 되므로 이를 pop()하여 리턴함
}
[실행결과]
case 1

case 2

case 3

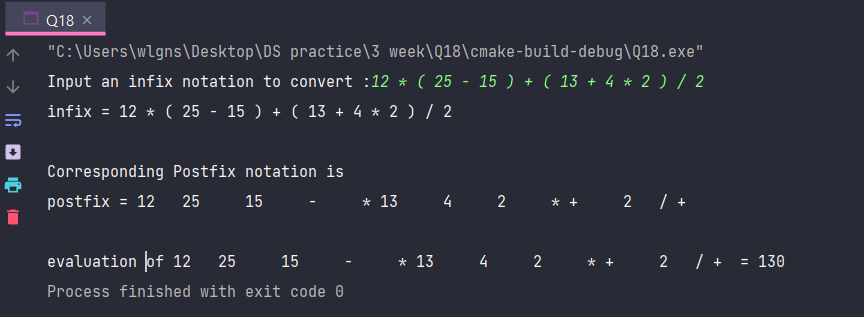
Q18. [실습] 중위 수식(infix) - 후위 수식(postfix) 변환 및 후위 수식 계산
주어진 조건을 만족하도록 중위 수식(infix)을 후위 수식(postfix)로 변환하여 계산하는 프로그램을 실행 화면을 참고하여 구현하시오
| 조건 | ||
| 1. 다음 수식과 같이 다중 숫자로 된 피연산자와 괄호를 포함하는 infix를 postfix로 변환한다. (예: 123 + ( 43 + 23 * 3 ) / 2 ) 2. 변환한 postfix를 출력하고 output_expr 문자열로 복사한다 3. output_expr에 저장된 postfix 수식을 eval 함수를 이용하여 평가한다 4. 최종 계산 결과를 출력한다 5. 실행 화면과 같이 다양한 예를 통하여 테스트한다 |
[실행화면]

[코드]
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#define MAX_STACK_SIZE 100
typedef enum { // 연산자
open_b, close_b, plus, minus, times, divide, mod, eos, operand
} priority;
void infix_to_postfix();
int precedence(char op);
char pop_token();
void push_token(char token);
int evaluate();
void push(int item);
int pop();
priority read_item(char *pointer);
int trans(char *n, int *index);
char infix[MAX_STACK_SIZE];
char post[MAX_STACK_SIZE];
char output_expr[MAX_STACK_SIZE];
int top=-1;
int token_top=-1;
char token_stack[MAX_STACK_SIZE];
int stack[MAX_STACK_SIZE];
char sym;
int sym_type;
int main(){
printf("Input an infix notation to convert :");
gets(infix);
printf("infix = %s\n\n", infix);
infix_to_postfix();
printf("Corresponding Postfix notation is\n");
printf("postfix = %s\n\n",post);
strcpy(output_expr, post);
printf("evaluation of %s = %d",output_expr,evaluate());
}
void infix_to_postfix(){
int i=0;
int pos=0;
while (infix[i] != '\0') { // '\0'이 아닐 때까지
if (infix[i] == '(') { // 열린괄호일때
push_token(infix[i]); // push
i++; // 다음
}
else if (infix[i] == ')') { // 닫힌괄호일때
sym = pop_token();
while (sym != '(') { // 열린괄호가 나올때까지
post[pos++]=sym;
post[pos++] = ' '; // 공백 담기
sym=pop_token();
}
i++;
}
else if (infix[i]>= '0' && infix[i] <= '9') { // 피연산자일 때
do {
post[pos++] = infix[i++]; // 숫자 넣음
} while (infix[i]>= '0' && infix[i] <= '9'); // 숫자가 끝날 때까지 (여러 자리 숫자)
post[pos++] = ' '; // 공백 담기
}
else { // 연산자일 때
while (precedence(token_stack[token_top])>=precedence(infix[i])&&token_top!=-1) { // 비어있지 않고 스택보다 우선순위가 낮다면
post[pos++]=pop_token(); // pop
post[pos++] = ' '; // 공백 담기
}
push_token(infix[i]); // 우선순위가 높으면 push
i++; // 다음
}
}
while (token_top!=-1) { // 스택이 비어있지 않을 때
post[pos++] = pop_token(); // 모두 post에 넣음
post[pos++] = ' '; // 공백 담기
}
post[pos]= '\0';
}
int precedence(char op){ // 우선 순위를 반환해 줌
if(op=='(') return 0; // 우선순위가 가장 낮음
if(op=='+' || op=='-') return 1;
if(op=='*' || op=='/' || op=='%') return 2;
}
void push_token(char token){
if(token_top<MAX_STACK_SIZE-1) token_stack[++token_top] = token;
else printf("token stack full\n");
}
char pop_token(){
if(token_top>=0) return token_stack[token_top--];
printf("token stack empty\n");
return ' ';
}
void push(int item){
if(top>=MAX_STACK_SIZE-1){
printf("stack full");
return ;
}
stack[++top]=item;
}
int pop(){
if(top<0){
printf("stack empty");
return -999;
}
return stack[top--];
}
priority read_item(char *pointer){
switch(*pointer){
case '(': sym_type = open_b; break;
case ')': sym_type = close_b; break;
case '+': sym_type = plus; break;
case '-': sym_type = minus; break;
case '*': sym_type = times; break;
case '/': sym_type = divide; break;
case '%': sym_type = mod; break;
case '\0': sym_type = eos; break;
default: sym_type = operand;
}
return sym_type;
}
int trans(char *n, int *index) { // 피연산자 정수 변환 함수
int result;
char temp[100];
int k, j;
for (k = 0; n[k] != ' '; k++) // 공백이 아닐 때까지 반복
temp[k] = n[k]; // temp에 피연산자 값을 담음
temp[k] = '\0'; // 끝에 '\0' 담음
result = atoi(temp); // 정수로 변환해 value에 저장
j = *index; // j에 index값 저장 (위에서 i값)
*index = j + k; // 피연산자 자릿수만큼 더해서 index(i)값 변환
return result; // 변환한 값 리턴
}
int evaluate(){
int value=0;
int op1, op2, i; // 연산자로 계산할 두 개의 숫자를 나타내는 변수 op1, op2
priority type;
for (i = 0; output_expr[i]!='\0';i++) {// post[i]이 '\0'이 아닐 때까지 반복
if(output_expr[i]==' '); // 공백이면 i 증가
else{
type = read_item(&output_expr[i]); // 문자 읽어오기
if (type == operand) {// sym이 숫자이면
value = trans(&output_expr[i],&i);
push(value); // atoi함수로 변환 한 수를 stack에 push함
}
else { // if의 조건이 아니며 expr에서 읽은 값이 ' ' 즉 띄어쓰기가 아닐 때 -> 연산자라는 의미임
op2 = pop();// op2()에 stack에서 값을 하나 꺼내 저장
op1 = pop();// op1()에 stack에서 다음 값을 하나 꺼내 저장
switch(type) {// sym이 case에 맞는다면 각 명령문에 맞게 계산을 진행
case plus: push(op1 + op2); break;
case minus: push(op1 - op2); break;
case times: push(op1 * op2); break;
case divide: push(op1 / op2); break;
case mod: push(op1 % op2); break;
}
}
}
}
return pop();// 계산이 끝나면 마지막에 stack에 남은 값이 우리가 계산한 결과값이 되므로 이를 pop()하여 리턴함
}
[실행결과]
'Study > Data Structure' 카테고리의 다른 글
| [DS] Linked List (연결 리스트) 와 Linked List Operator ( 연결 리스트 연산자) (0) | 2021.09.07 |
|---|---|
| [DS] A Maze Problem (스택으로 미로 문제 풀기) (2) | 2021.09.02 |
| [DS] Deque (Double-ended-queue) (0) | 2021.09.02 |
| [DS] Evaluation of expression (수식의 평가) (0) | 2021.09.02 |
| [DS] Queue(큐) & Circular Queue(순환 큐) (0) | 2021.08.31 |
